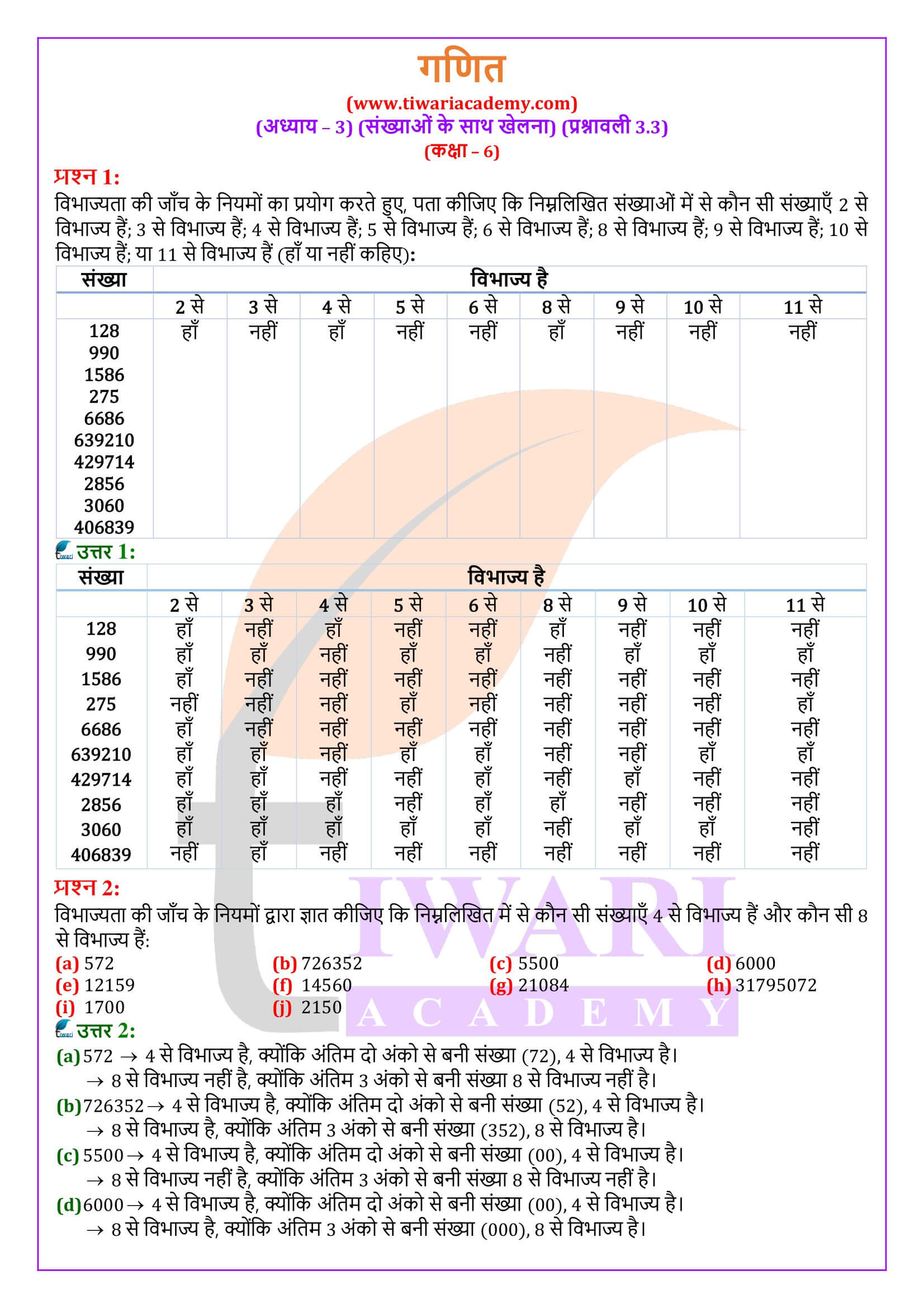
एनसीईआरटी समाधान कक्षा 6 गणित प्रश्नावली 3.3
एनसीईआरटी समाधान कक्षा 6 गणित प्रश्नावली 3.3 संख्याओं के साथ खेलना के हल पुस्तक के अभ्यास में दिए गए सवाल जवाब सत्र 2025-26 के लिए यहाँ दिए गए हैं। कक्षा 6 गणित के छात्र प्रश्नावली 3.3 की तैयारी यहाँ दिए गए विडियो समाधान की मदद से आसानी से कर सकते हैं।
एनसीईआरटी समाधान कक्षा 6 गणित प्रश्नावली 3.3
एनसीईआरटी समाधान कक्षा 6 गणित प्रश्नावली 3.3 संख्याओं के साथ खेलना
संख्याओं की विभाज्यता की जाँच
आइए देखें कि क्या हम कोई प्रतिरूप (पैटर्न) ज्ञात कर सकते हैं जिससे हम बता सकें कि कोई संख्या 2ए 3ए 4ए 5ए 6ए 8ए 9ए 10 या 11 से विभाज्य है या नहीं। क्या आप सोचते हैं कि ऐसे प्रतिरूप हम आसानी से देख सकते हैं?
10 से विभाज्यता:
10 के गुणजों 10, 20, 30, 40, 50, 60, — को देख रही थी। उसने इन संख्याओं में एक सर्वनिष्ठ गुण देखा। क्या आप बता सकते हैं कि वह गुण क्या है? इनमें प्रत्येक के इकाई के स्थान पर अंक 0 है।
उसने इकाई के स्थान 0 वाली कुछ और संख्याओं के बारे में भी सोचा, जैसे कि 100, 1000 3200 7010 आदि। उसने यह भी ज्ञात किया कि ये सभी संख्याएँ 10 से विभाज्य हैं।
इस प्रकार, वह ज्ञात करती है कि यदि किसी संख्या के इकाई के स्थान पर अंक 0 हो, तो वह 10 से विभाज्य होती है।
5 से विभाज्यता:
मनि ने संख्याओं 5, 10, 15, 20, 25, 30, 35, — में एक रोचक प्रतिरूप प्राप्त किया। क्या आप यह प्रतिरूप बता सकते हैं? इन सभी संख्याओं में, इकाई के स्थान पर या तो अंक 0 है या अंक 5 है। उसने ज्ञात किया कि ये सभी संख्याएँ 5 से विभाज्य हैं।
यदि किसी संख्या का इकाई का अंक 0 हो या 5 हो, तो वह संख्या 5 से विभाज्य होती है।
2 से विभाज्यता
2 के कुछ गुणजों 10, 12, 14, 16, — और कुछ अन्य गुणजों जैसे 2410, 4356, 1358, 2972, 5974 को देखती है। उसे इनमें एक प्रतिरूप दिखाई देता है। क्या आप इस प्रतिरूप को बता सकते हैं? इन संख्याओं के इकाई के स्थान पर 0, 2, 4, 6 और 8 में से ही कोई अंक आता है।
यदि किसी संख्या के इकाई के स्थान पर 0, 2, 4, 6 या 8 में से कोई अंक हो, तो वह संख्या 2 से विभाज्य होती है।
3 से विभाज्यता
क्या संख्या 21, 27, 36, 54 और 219 संख्या 3 से विभाज्य हैं? हाँ, ये हैं।
क्या संख्याएँ 25, 37 और 260 संख्या 3 से विभाज्य हैं? नहीं।
3 से विभाज्यता के लिए क्या आप कोई प्रतिरूप इकाई स्थान में देख सकते हैं हम नहीं
देख सकते, क्योंकि इकाई के स्थान पर समान अंक होने पर वह 3 से विभाजित हो भी सकता है और नहीं भी। जैसे संख्या 27, 3 से विभाजित है, पर संख्याएँ 17, 37, 3 से विभाजित नहीं है।
अब आप 21, 36, 54 और 219 के अंकों को जोडि़ए। क्या आप इनमें कोई विशेष बात देखते हैं? 2 + 1 = 3, 3 + 6 = 9, 5 + 4 = 9, 2 + 1 + 9 = 12। ये सभी योग 3 से विभाज्य हैं।
25, 37, 260 के अंकों को जोडि़ए। हमें 2 + 5 = 7, 3 + 7 = 10, 2 + 6 + 0 = 8 प्राप्त होता है। इनमें से कोई भी योग 3 से विभाज्य नहीं है।
हम कहते हैं कि यदि किसी संख्या के अंकों का योग 3 का एक गुणज हो, तो वह संख्या 3 से विभाज्य होती है।