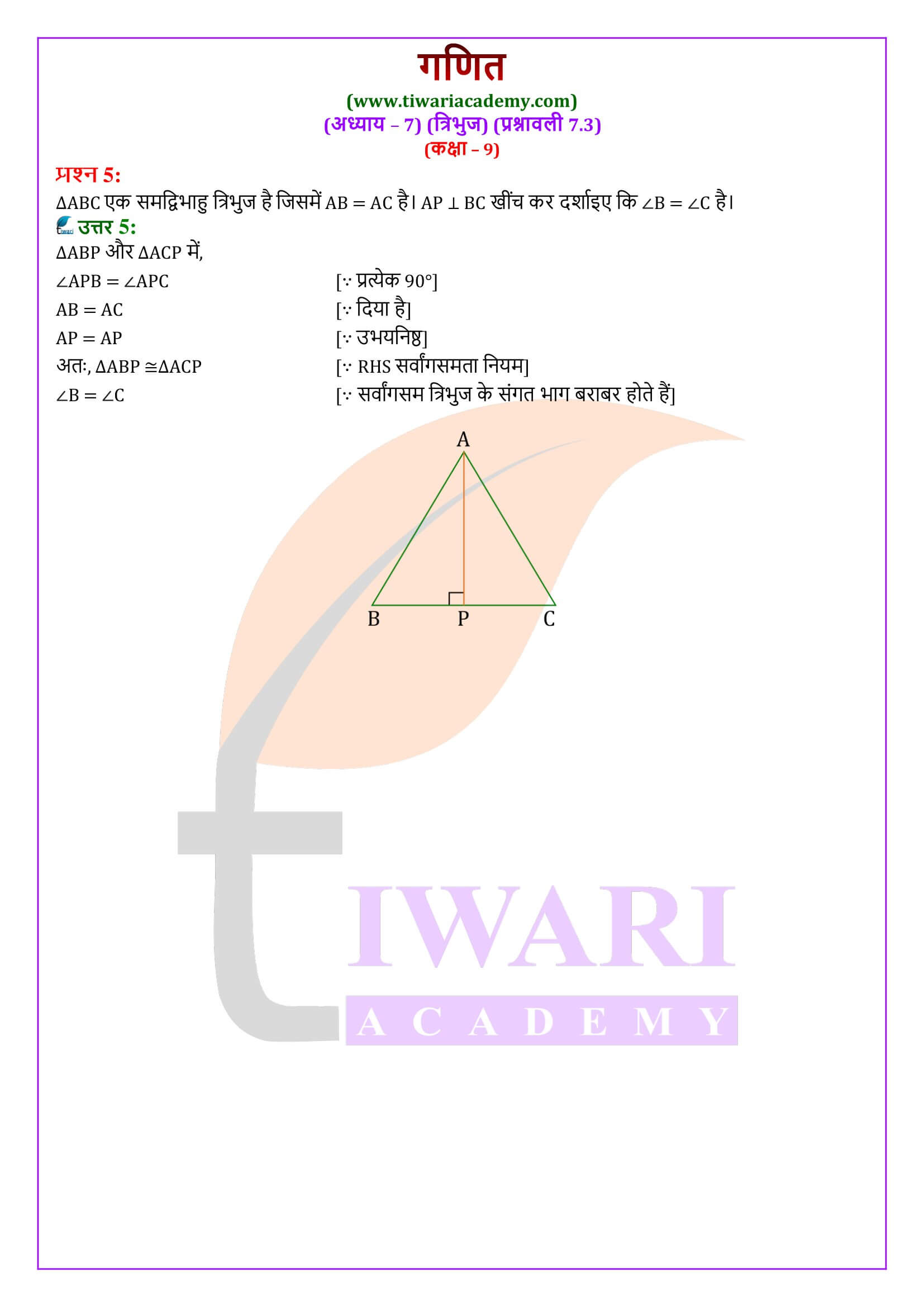
एनसीईआरटी समाधान कक्षा 9 गणित प्रश्नावली 7.3

एक त्रिभुज के तीनों कोणों के दूसरे त्रिभुज के तीनों कोणों के बराबर होने पर दोनों त्रिभुजों का सर्वांगसम होना आवश्यक नहीं है। इसके लिए कुछ और भी नियम हैं जो निम्न प्रकार से हैं:
प्रमेय 7.4 (SSS सर्वांगसमता नियम):
यदि एक त्रिभुज की तीनों भुजाएँ एक अन्य त्रिभुज की तीनों भुजाओं के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं। दूसरे शब्दों में दोनों त्रिभुज एक दूसरे को पूर्णतया ढक लेते हैं और इसीलिए ये सर्वांगसम हैं।

यदि दो समकोण त्रिभुजों में, एक त्रिभुज का कर्ण और एक भुजा क्रमशः दूसरे त्रिभुज के कर्ण और एक भुजा के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं।
ध्यान दीजिए कि यहाँ RHS समकोण – कर्ण – भुजा को दर्शाता है।

AB एक रेखाखंड है तथा बिंदु P और Q इस रेखाखंड AB के विपरीत ओर इस प्रकार स्थित हैं कि इनमें से प्रत्येक A और B से समदूरस्थ है। दर्शाइए कि रेखा PQ रेखाखंड AB का लम्ब समद्विभाजक है।
हल:
आपको PA = PB और QA = QB दिया हुआ है।
आपको दर्शाना है कि PQ ⊥ AB है और PQ रेखाखंड AB को समद्विभाजित करती है। मान लीजिए रेखा PQ रेखाखंड AB को C पर प्रतिच्छेद करती है।
यहाँ पर ∆ PAQ और ∆ PBQ लेते हैं।
इन त्रिभुजों में
AP = BP (दिया है)
AQ = BQ (दिया है)
PQ =PQ (उभयनिष्ठ हैं)
अतः, D PAQ ≅ D PBQ (SSS नियम)
इसलिए, ∠ APQ = ∠ BPQ (CPCT)
अब ∆ PAC और ∆ PBC लेते हैं। आपको प्राप्त है:
AP =BP (दिया है)
∠ APC = ∠ BPC (∠ APQ = ∠ BPQ पहले सिद्ध किया जा चुका है)
PC =PC (उभयनिष्ठ)

अतः ∆ PAC ≅ ∆ PBC (SAS नियम)
इसलिए, AC = BC (CPCT) (1)
और ∠ ACP = ∠ BCP (CPCT)
साथ ही ∠ ACP + ∠ BCP = 180° (रैखिक युग्म)
इसलिए, 2∠ ACP = 180°
या ∠ ACP = 90° (2)
(1) और (2) से, आप निष्कर्ष निकाल सकते हैं कि रेखा PQ रेखाखंड AB का लम्ब समद्विभाजक है।

1. यदि एक त्रिभुज के दो कोण और अंतर्गत भुजा दूसरे त्रिभुज के दो कोणों और अंतर्गत भुजा के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं।
2. यदि एक त्रिभुज के दो कोण और एक भुजा दूसरे त्रिभुज के दो कोणों और संगत भुजा के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं (AAS सर्वांगसमता नियम)।