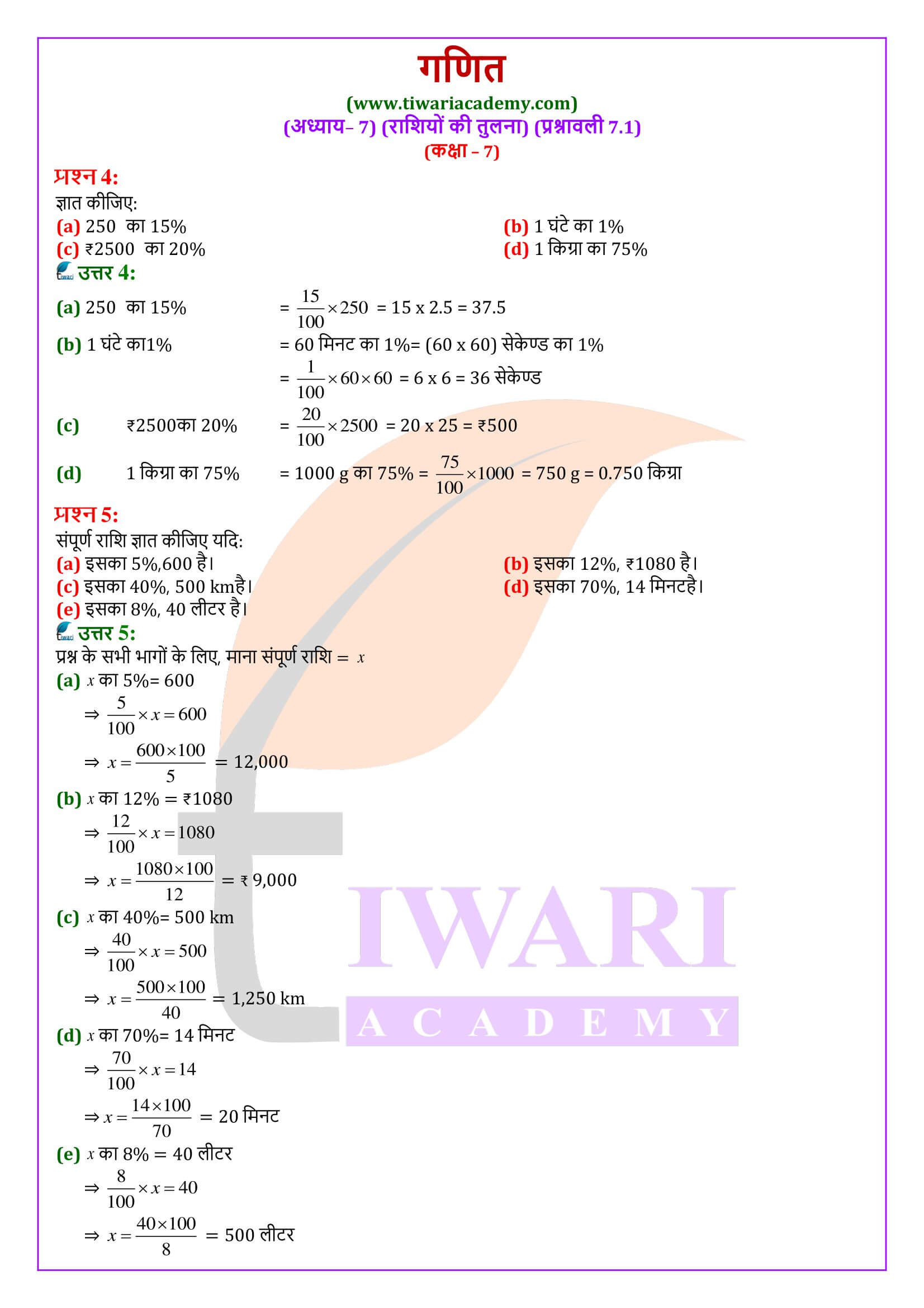
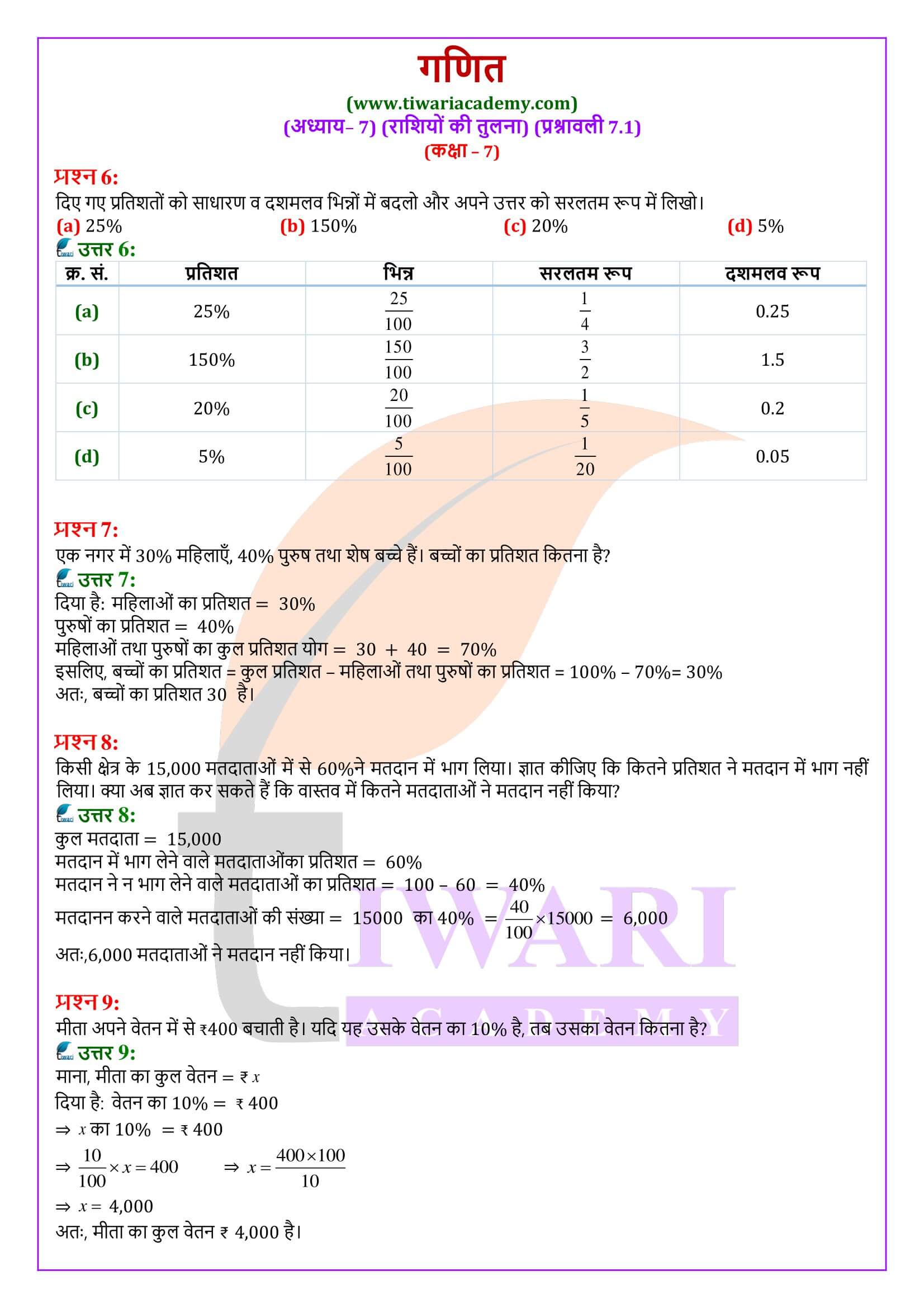
एनसीईआरटी समाधान कक्षा 7 गणित प्रश्नावली 7.1
एनसीईआरटी समाधान कक्षा 7 गणित प्रश्नावली 7.1 राशियों की तुलना के प्रश्नों के उत्तर अभ्यस के सभी सवाल जवाब सीबीएसई तथा राजकीय बोर्ड सत्र 2025-26 के लिए यहाँ दिए गए हैं। कक्षा 7 गणित अध्याय 7.1 के सभी प्रश्नों के हल यहाँ से विस्तार में प्राप्त किए जा सकते हैं। प्रश्नों को सहज रूप से हल करके विडियो समाधान के रूप में भी दिया गया है।
एनसीईआरटी समाधान कक्षा 7 गणित प्रश्नावली 7.1
कक्षा 7 गणित प्रश्नावली 7.1 राशियों की तुलना के प्रश्नों के हल
प्रतिशतता-राशियों के तुलना करने की एक और विधि
प्रतिशत उन भिन्नों का अंश होता है जिनका हर 100 होता है, और यहाँ पर परीक्षाफलों की तुलना करने में इसे किया गया है।
अनीता कहती है कि उसका परीक्षाफल अधिक अच्छा है, क्योंकि उसने 320 अंक प्राप्त किए है जबकि रीता ने केवल 300 अंक। क्या आप उससे सहमत हैं? आपके विचार में किसका परीक्षाफल अधिक अच्छा है?
मानसी कहती है कि केवल प्राप्तांकों की तुलना कर यह नहीं कहा जा सकता है कि किसका परीक्षाफल अधिक अच्छा है क्योंकि अधिकतम अंक जिनमें से दोनों को अंक प्राप्त हुए हैं वे समान नहीं हैं।
वह कहती है कि रिपोर्ट कार्डों में दिए गए प्रतिशत अंकों पर आप ध्यान क्यों नहीं देती। अनीता के प्रतिशत अंक 80 हैं जबकि रीता के प्रतिशत अंक 83.3 हैं। इससे पता चलता है कि रीता का परीक्षाफल अधिक अच्छा है।
प्रतिशतता के अर्थ
प्रतिशत शब्द, लेटिन भाषा के एक शब्द परसेंटम से लिया गया है जिसका अर्थ है ‘प्रति एक सौ’।
प्रतिशत को चिह्न % से प्रदर्शित किया जाता है जिसका अर्थ हैं सौवाँ। यानी एक सौवाँ अर्थात् 1% का अर्थ है सौ में से एक अथवा एक सौवाँ। इसे इस प्रकार लिखते हैंः
1% = 1/100
= 0.01
भिन्न संख्याओं को प्रतिशत में बदलना
भिन्न संख्याओं में, हर विभिन्न संख्याएँ हो सकती हैं। उनकी तुलना करने के लिए हमें उनके हरों को समान करना पड़ता है और हम देख चुके हैं कि तब उनकी तुलना करना बहुत आसान जाता है यदि उनमें प्रत्येक का हर 100 हो। यानी हम भिन्नों को प्रतिशत में बदल रहे हैं। आइए अब कुछ भिन्नों को प्रतिशत में बदलने का प्रयत्न करें।
उदाहरण:
1/3 को प्रतिशत रूप में लिखिए।
हल:
संख्या है 1/3 = 1/3 × 100/100 = 1/3 × 100%
= 100/3 % = 33(1/3)%
दशमलव भिन्न को प्रतिशत में बदलना
हमने देखा कि साधारण भिन्नों को प्रतिशत में किस प्रकार बदला जाता है। अब आइए देखें दशमलव भिन्नों को भी प्रतिशत में कैसे बदला जाता है।
अभ्यास 7.1 के लिए प्रश्न उत्तर
दिए गए दशमलवों को प्रतिशत में बदलिए:
(a) 0.75
(b) 0.09
(c) 0.2
हल:
(a) 0.75 = 0.75 × 100%
75/100 × 100 % = 75%
(b) 0.09 = 9/100
= 9 %
(c) 0.2 = 2/10 × 100%
= 20 %
प्रतिशत को साधारण भिन्न या दशमलव में बदलना
अभी तक हमने साधारण भिन्न या दशमलव भिन्न को प्रतिशत में बदला। हम इसका विपरीत भी कर सकते हैं। यानी, प्रतिशत दिए होने पर उसे साधारण या दशमलव भिन्न में भी बदल सकते हैं।
1% = 1/100 = 0.01, 10% = 1/10 = 0.1
निम्न उदाहरण पर विचार कीजिएः
विद्यार्थियों की दी गई संख्या में 30% लड़के हैं।
इसका अर्थ यह हुआ कि यदि 100 विद्यार्थी हैं तो उनमें 30 लड़के हैं तथा शेष लड़कियाँ होंगी ।
स्पष्ट है कि लड़कियाँ होंगी (100-30)% = 70%