एनसीईआरटी समाधान कक्षा 7 गणित प्रश्नावली 3.1
एनसीईआरटी समाधान कक्षा 7 गणित प्रश्नावली 3.1 आँकड़ो का प्रबंधन के प्रश्नों के हल हिंदी और अंग्रेजी माध्यम में सवाल जवाब सत्र 2025-26 के लिए यहाँ दिए गए हैं। कक्षा 7 गणित अध्याय 3.1 के हल सीबीएसई के साथ-साथ राजकीय बोर्ड के उन छात्रों के लिए भी उपयोगी हैं जो एनसीईआरटी पुस्तक से अपना पाठ्यक्रम पढ़ रहें हैं।
एनसीईआरटी समाधान कक्षा 7 गणित प्रश्नावली 3.1
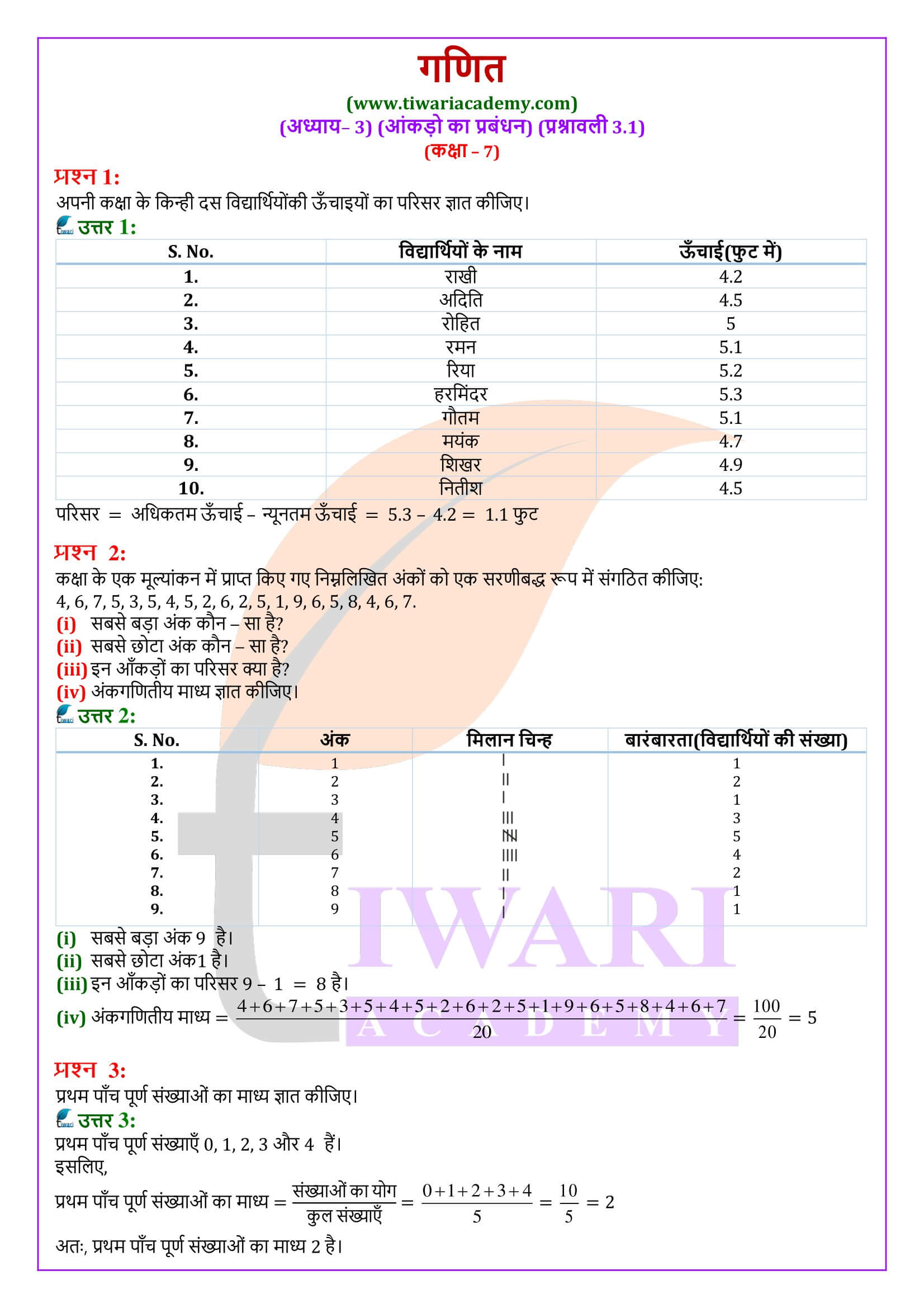
कक्षा 7 गणित प्रश्नावली 3.1 आँकड़ो का प्रबंधन के प्रश्नों के हल
आंकड़े और उनका प्रारूप
प्राय हम रोजाना समाचार पत्रों और न्यूज़ में मौसम संबंधी जानकारी पढ़ते हैं या किसी फूटबाल लीग में खेलने वाली टीमों ने किसने किसको कितने गोल से हराया या हम सप्ताह में किसी कक्षा में उपस्थित होने वाले छात्रों के आंकड़े। आप समाचार-पत्रें, पत्रिकाओं, टेलीविजन और अन्य साधनों से, विभिन्न प्रकार के आँकड़ों को देख चुके हैं। आप यह भी जानते हैं कि सभी आँकड़े हमें किसी न किसी प्रकार की सूचना अवश्य देते हैं। आइए आँकड़ों के कुछ सामान्य रूपों को देखें, जो आपके सम्मुख आते रहते हैं।
नगरों के तापमान 20.6.2006 को
शहर का नाम – अधिकतम – न्यूनतम
अहमदाबाद – 38°C – 29°C
अमृतसर – 37°C – 26°C
बेंगलूर – 28°C – 21°C
चेन्नई – 36°C – 27°C
दिल्ली – 38°C – 28°C
जयपुर – 39°C – 29°C
जम्मू – 41°C – 26°C
मुंबई – 32°C – 27°C
उपरोक्त सारणी से आप यह कह सकते हैं कि 20-6-2006 को जम्मू का अधिकतम तापमान सबसे अधिक था।
एक कक्षा में साप्ताहिक अनुपस्थिति दर्शाने वाले आँकड़े
साप्ताहिक दिन – अनुपस्थित छात्रों की संख्या
सोमवार – 3
मंगलवार – 1
बुधवार – 0
बृहस्पतिवार – 5
शुक्रवार – 2
शनिवार – 4
हम कह सकते हैं कि बुधवार को कोई बच्चा अनुपस्थित नहीं था।
आँकड़ों का संग्रह
आँकड़ों को इकट्ठे करने से पहले, हमें यह जानना आवश्यक है कि हम इनका उपयोग किसके लिए करेंगे।
नीचे कुछ स्थितियाँ दी जा रही हैं।
आप अध्ययन करना चाहते हैं:
(a) गणित में अपनी कक्षा के प्रदर्शन का
(b) फुटबॉल या क्रिकेट में भारत के प्रदर्शन का
(c) किसी क्षेत्र में महिला साक्षरता दर का, अथवा
(d) आपके आस-पास के परिवारों में 5 वर्ष से कम आयु के बच्चों की संख्या का।
उपरोक्त स्थितियों में, आपको किस प्रकार के आँकड़ों की आवश्यकता है? जब तक आप उपयुक्त आँकड़े इकट्ठे नहीं करेंगे, आप वांछित जानकारी नहीं प्राप्त कर सकते हैं। प्रत्येक के लिए, उपयुक्त आँकड़े क्या हैं?
प्रतिनिधि मान
औसत एक ऐसी संख्या है जो प्रेक्षणों या आँकड़ों के एक समूह की केंद्रीय प्रवृत्ति को निरूपित करती (या दर्शाती) है। क्योंकि औसत सबसे अधिक तथा सबसे कम मूल्य के आँकड़ों के बीच में होता है। इसलिए हम कहते हैं कि औसत, आँकड़ों के एक समूह की केंद्रीय प्रवृत्ति का मापक है। विभिन्न प्रकार के आँकड़ों की व्याख्या करने के लिए, विभिन्न प्रकार के प्रतिनिधि या केंद्रीय मानों की आवश्यकता होती है। इनमें से एक प्रतिनिधि मान अंकगणितीय माध्य या समांतर माध्य है।
आँकड़ों का संगठन
जब हम आँकड़ों को संग्रहित करते हैं, तो हमें उन्हें रिकॉर्ड करके संगठित करना होता है। हमें इसकी क्यों आवश्यकता पड़ती है? निम्न उदाहरण पर विचार कीजिएः
कक्षा अध्यापिका सुश्री नीलम यह जानना चाहती थी कि अंग्रेजी में बच्चों का प्रदर्शन कैसा रहा? वह विद्यार्थियों द्वारा प्राप्त अंकों को निम्नलिखित प्रकार से लिखती हैः
23, 35, 48, 30, 25, 46, 13, 27, 32, 38
इस रूप में, आँकड़े सरलता से समझने योग्य नहीं थे। इस तरह नीलम यह समझ सकी कि किस छात्र ने कितने अंक प्राप्त किए। लेकिन वह कुछ और जानकारी चाहती थी। दीपिका ने उन आँकड़ों को दूसरी तरह से प्रदर्शित किया।
अंकगणितीय माध्य
आँकड़ों के एक समूह के लिए अंधिकांशतः प्रयोग किए जाना वाला प्रतिनिधि मान अंकगणितीय माध्य है, संक्षेप में इसे माध्य (उमंद) भी कहते हैं।
उदाहरण
दो बर्तनों में क्रमशः 20 लीटर और 60 लीटर दूध है। यदि दोनों बर्तनों में बराबर-बराबर दूध रखा जाए, तो प्रत्येक बर्तन में कितना दूध होगा? जब हम इस प्रकार का प्रश्न पूछते हैं, तब हम अंकगणितीय माध्य ज्ञात करने के लिए कहते हैं।
उपरोक्त स्थिति में, औसत या अंकगणितीय माध्य होगा:
= दूध की कुल मात्रा / बर्तनों की संख्या = (20 + 60)/2 लीटर = 40 लीटर
इस प्रकार, प्रत्येक बर्तन में 40 लीटर दूध होगा।
औसत या अंकगणितीय माध्य (।ण्डण्) या केवल माध्य को निम्नलिखित रूप से परिभाषित किया जाता हैः
माध्य = सभी प्रेक्षणों का योग / प्रेक्षणों की संख्या