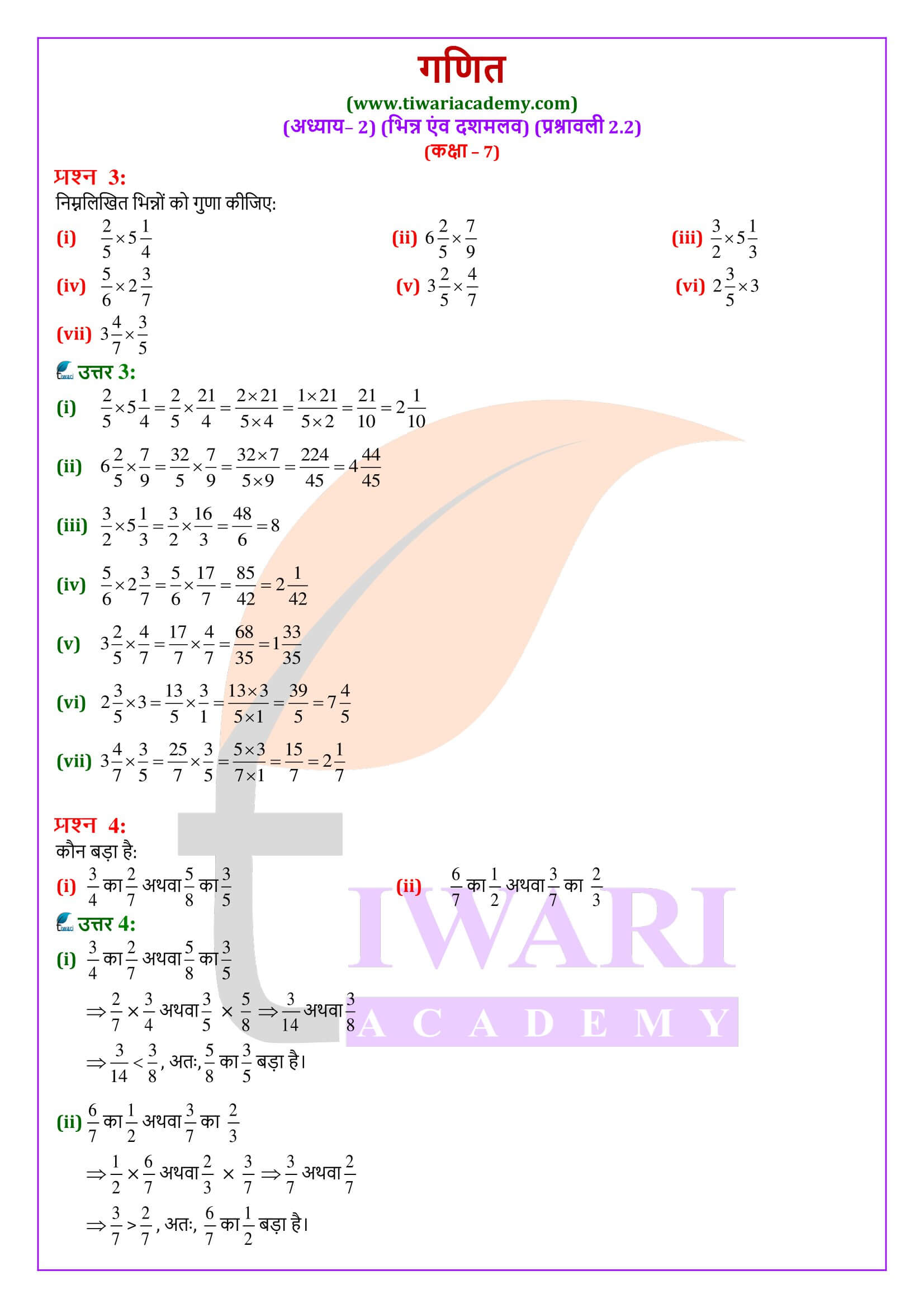
एनसीईआरटी समाधान कक्षा 7 गणित प्रश्नावली 2.2

जब दो उचित भिन्नों को गुणा किया जाता है तो गुणनफल दोनों भिन्नों से कम होता है।
उदाहरण:
फरीदा के पास 9 cm लंबी एक रिबन की पट्टी थी। उसने इस पट्टी को चार समान भागों में काटा। उसने यह किस प्रकार किया? उसने पट्टी को दो बार मोड़ा। प्रत्येक भाग कुल लंबाई के किस भिन्न को निरूपित करेगा। प्रत्येक भाग, पट्टी का 9/4 होगा। उसने इनमें से एक भाग लिया और इस भाग को एक बार मोड़ते हुए इसे दो बराबर भागों में बाँट दिया। क्या आप जानते हैं कि इन दो टुकड़ों में से एक टुकड़ा क्या निरूपित करेगा?
जी हाँ, यह 9/4 का ½ अर्थात् ½ × 9/4 को निरूपित करेगा।

आइए देखते हैं कि दो भिन्नों का गुणनफल जैसे ½ × 9/4 को कैसे ज्ञात किया जाए।
इसे ज्ञात करने के लिए आइए सर्वप्रथम हम ½ × 1/3 जैसा गुणनफल ज्ञात करना सीखते हैं।
½ × 1/3 का मान भी इसी प्रकार ज्ञात किया जा सकता है। संपूर्ण को 2 समान भागों में बाँटिए और तब इनमें से किसी एक भाग को 3 समान भागों में बाँटिए। इनमें से एक भाग को लीजिए। यह 1/3 × ½ अर्थात् 1/6 भाग को निरूपित करेगा।
इस प्रकार, 1/3 × ½ = (1 × 1)/(3 × 2) = 1/6
इस प्रकार हम पाते हैं कि हम दो भिन्नों का गुणन = अंशों का गुणनफल/ हरों का गुणनफल

दो उचित भिन्नों के गुणनफल का मान दोनों भिन्नों में से प्रत्येक से छोटा होता है। लेकिन दो विषम भिन्नों का गुणनफल उनमें से प्रत्येक भिन्न से बड़ा है। अथवा दो विषम भिन्नों के गुणनफल का मान उनमें से प्रत्येक भिन्न से अधिक है।
उदाहरण:
(i) 2/3 × 4/5 = 8/15 यहाँ 2/3 > 8/15 और 4/5 > 8/15 यह उचित भिन्न के लिए है।
(ii) 7/3 × 5/2 = 35/6 यहाँ 35/6 > 7/3 और 35/6 > 5/2 यह विषम भिन्न के लिए है।