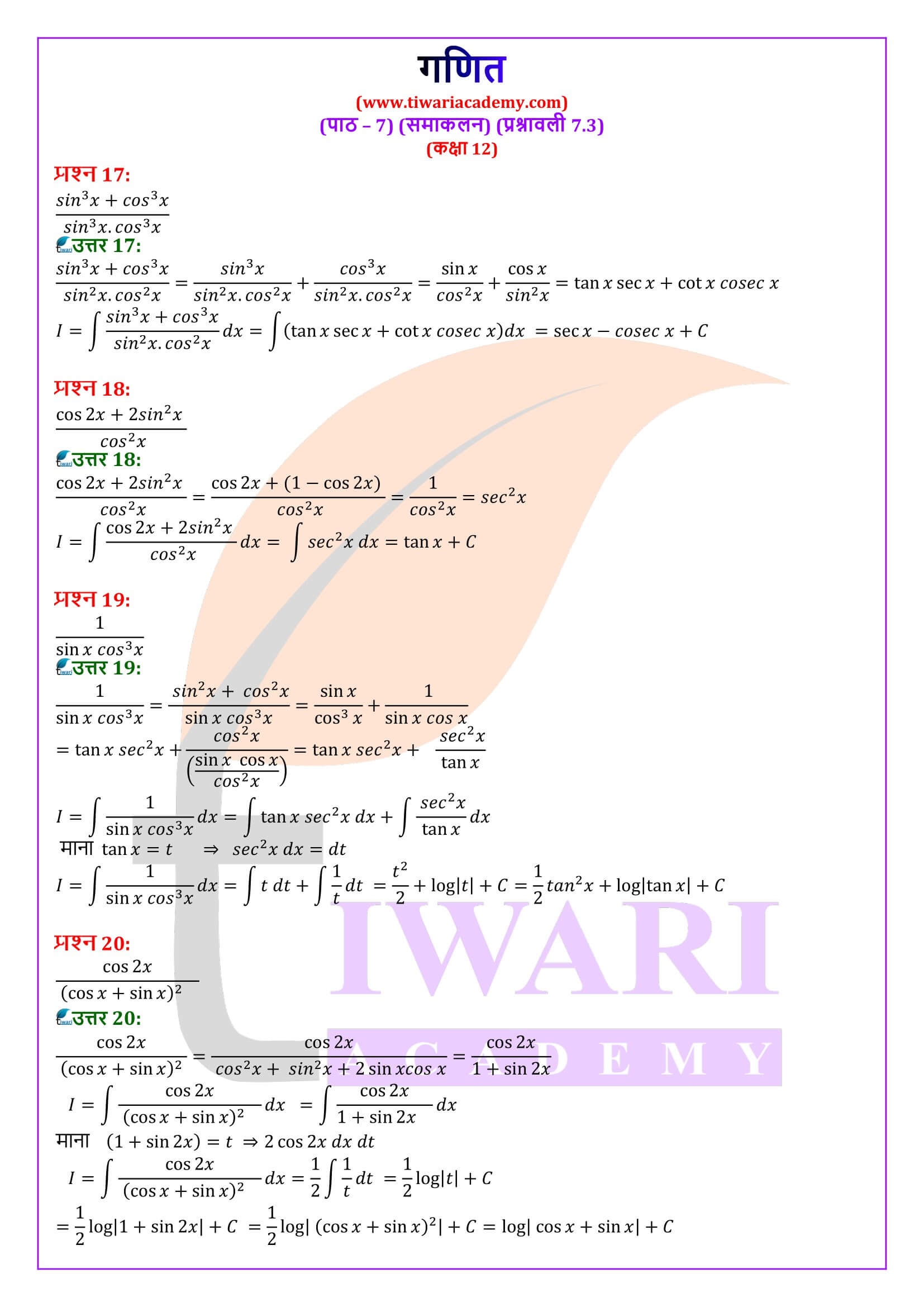
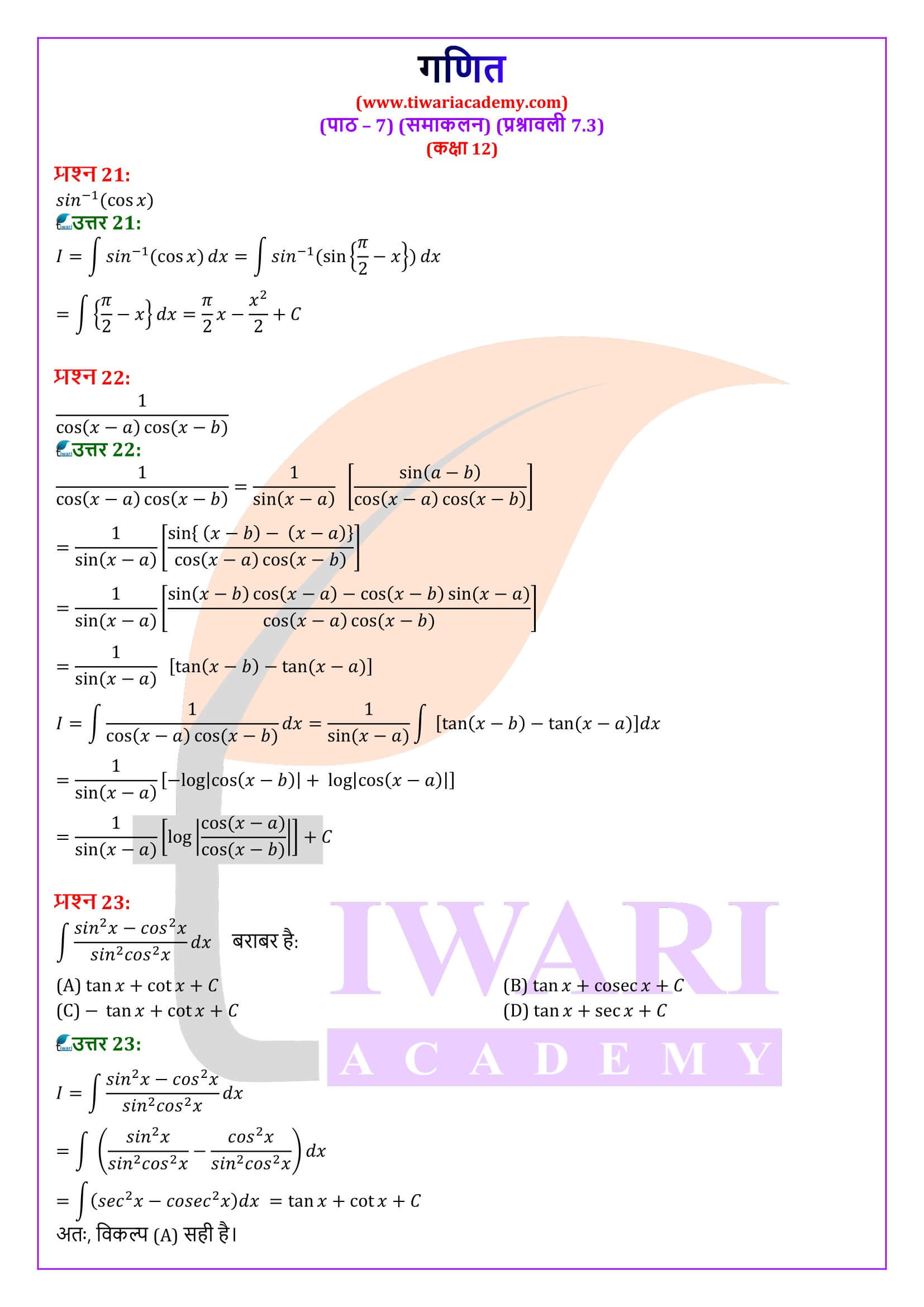
एनसीईआरटी समाधान कक्षा 12 गणित अध्याय 7 प्रश्नावली 7.3
एनसीईआरटी समाधान कक्षा 12 गणित अध्याय 7 प्रश्नावली 7.3 समाकलन के अभ्यास में दिए गए सभी सवालों के जवाब हल सहित सत्र 2025-26 के लिए यहाँ से प्राप्त किए जा सकते हैं। 12वीं कक्षा गणित की एक्सरसाइज 7.3 त्रिकोणमितीय फलनों के समाकलन पर आधारित है। अतः, छात्र त्रिकोणमितीय सूत्रों को ध्यान से याद कर लें।
कक्षा 12 गणित प्रश्नावली 7.3 के लिए एनसीईआरटी समाधान
त्रिकोणमितीय सर्व-समिकाओं के उपयोग द्वारा समाकलन
त्रिकोणमितीय सर्व-समिकाओं के उपयोग द्वारा समाकलन एकीकरण का उपयोग करके किया जा सकता है। हम इन सर्वसमिकाओं का उपयोग करके समाकलन को कम कर सकते हैं और समाकल का मूल्यांकन करना आसान बना सकते हैं। उदाहरण के लिए, उत्पाद-से-योग पहचान का उपयोग sin^nx cos^mdx के अभिन्न का आकलन करने के लिए किया जा सकता है। इस पद्धति को जानने से हम वक्र के अंतर्गत क्षेत्र और परिवर्तन की दरों से संबंधित समस्याओं के लिए इसका उपयोग करने में सक्षम होंगे।
कक्षा 12 गणित की प्रश्नावली 7.3 का परिचय
एनसीईआरटी कक्षा 12 प्रश्नावली 7.3 में समस्याओं की एक श्रृंखला शामिल है जो छात्रों को निश्चित अभिन्नों को समझने और उनकी समस्या को सुलझाने के कौशल विकसित करने में मदद करती है। प्रश्नावली का उद्देश्य छात्रों को अध्याय 7 में सीखी गई एकीकरण विधियों का अभ्यास शुरू करने और उन्हें लागू करने में मदद करना है। समस्याओं को हल करने के लिए, छात्रों को बीजगणित, त्रिकोणमिति और ज्यामिति के अपने ज्ञान को विकसित करने की भी आवश्यकता होगी।
कक्षा 12 गणित प्रश्नावली 7.3 के प्रश्न
प्रश्नावली 7.3 में अनेक प्रश्नों का उद्देश्य निश्चित समाकलों के विचारों को समझने और उनका उपयोग करने में विद्यार्थियों की सहायता करना है। एकीकरण के तरीकों जैसे प्रतिस्थापन, भागों द्वारा एकीकरण, और मानक सूत्र एकीकरण से संबंधित प्रश्नों का उपयोग करके एक फलन के रूप में प्राप्त करना निश्चित है। समस्याओं को हल करने के लिए, छात्रों को बीजगणित, त्रिकोणमिति और ज्यामिति की अपनी समझ का भी उपयोग करने की आवश्यकता होगी।
कक्षा 12 गणित प्रश्नावली 7.3 के मुख्य बिंदु
प्रश्नावली 7.3 में विभिन्न प्रकार की समस्याएं शामिल हैं जिनमें निश्चित समाकलों का मूल्यांकन, वक्र के अंतर्गत क्षेत्र का निर्धारण और वास्तविक दुनिया की समस्याओं का समाधान शामिल है। प्रश्नावली का उद्देश्य छात्रों को प्रतिस्थापन, भागों द्वारा एकीकरण, और त्रिकोणमितीय पहचान जैसे एकीकरण विधियों का अभ्यास करने और लागू करने में सहायता करना है। समस्याओं को हल करने के लिए, छात्रों को बीजगणित, त्रिकोणमिति और ज्यामिति के अपने ज्ञान को भी विकसित करना होगा।
प्रश्नावली 7.3 में प्रयोग होने वाले सूत्र
यह ध्यान रखना महत्वपूर्ण है कि प्रश्नावली 7.3 में प्रयुक्त विशेष सूत्रों के आधार पर हल की जा रही समस्या या प्रश्न अलग-अलग होंगे। ये कुछ समीकरण हैं जिनका प्रयोग प्रश्नावली 7.3 में किया गया होगा।
निश्चित अभिन्न की रैखिकता: ∫(af(x) + bg(x)) dx = a ∫f(x) dx + b ∫g(x) dx
» निश्चित अभिन्न के लिए प्रतिस्थापन नियम: ∫f(g(x))g'(x) dx = ∫f(u)du
» भागों द्वारा एकीकरण: ∫udv = uv – ∫v*du
» त्रिकोणमितीय पहचान: ∫sin^n(x)dx = -cos(x)sin^(n-1)(x)/(n-1) + (n-2) ∫sin^(n-2)(x) dx
» मानक सूत्र: ∫1/x^n dx = x^(1-n) / (1-n) जहां n 1 के बराबर नहीं है
» आयतन: V = ∫(ऊपरी सीमा – निचली सीमा) π*f(x)^2 dx