एनसीईआरटी समाधान कक्षा 12 गणित अध्याय 2 विविध प्रश्नावली
एनसीईआरटी समाधान कक्षा 12 गणित अध्याय 2 विविध प्रश्नावली 2 प्रतिलोम त्रिकोणमितीय फलन के सभी सवालों के जवाब हिंदी या अंग्रेजी मीडियम में विद्यार्थी यहाँ से प्राप्त कर सकते हैं। कक्षा 12 के गणित के छात्र सभी समाधानों को विडियो के रूप में भी मुफ्त डाउनलोड कर सकते हैं। विडियो और पीडीएफ दोनों प्रकार के समाधान सरल भाषा में तैयार किए गए हैं ताकि छात्रों को इसे समझने में कोई परेशानी न हो।
एनसीईआरटी समाधान कक्षा 12 गणित विविध प्रश्नावली 2
कक्षा 12 गणित अध्याय 2 विविध प्रश्नावली 2 प्रतिलोम त्रिकोणमितीय फलन एनसीईआरटी समाधान
प्रतिलोम त्रिकोणमितीय फलनों के गुणधर्म
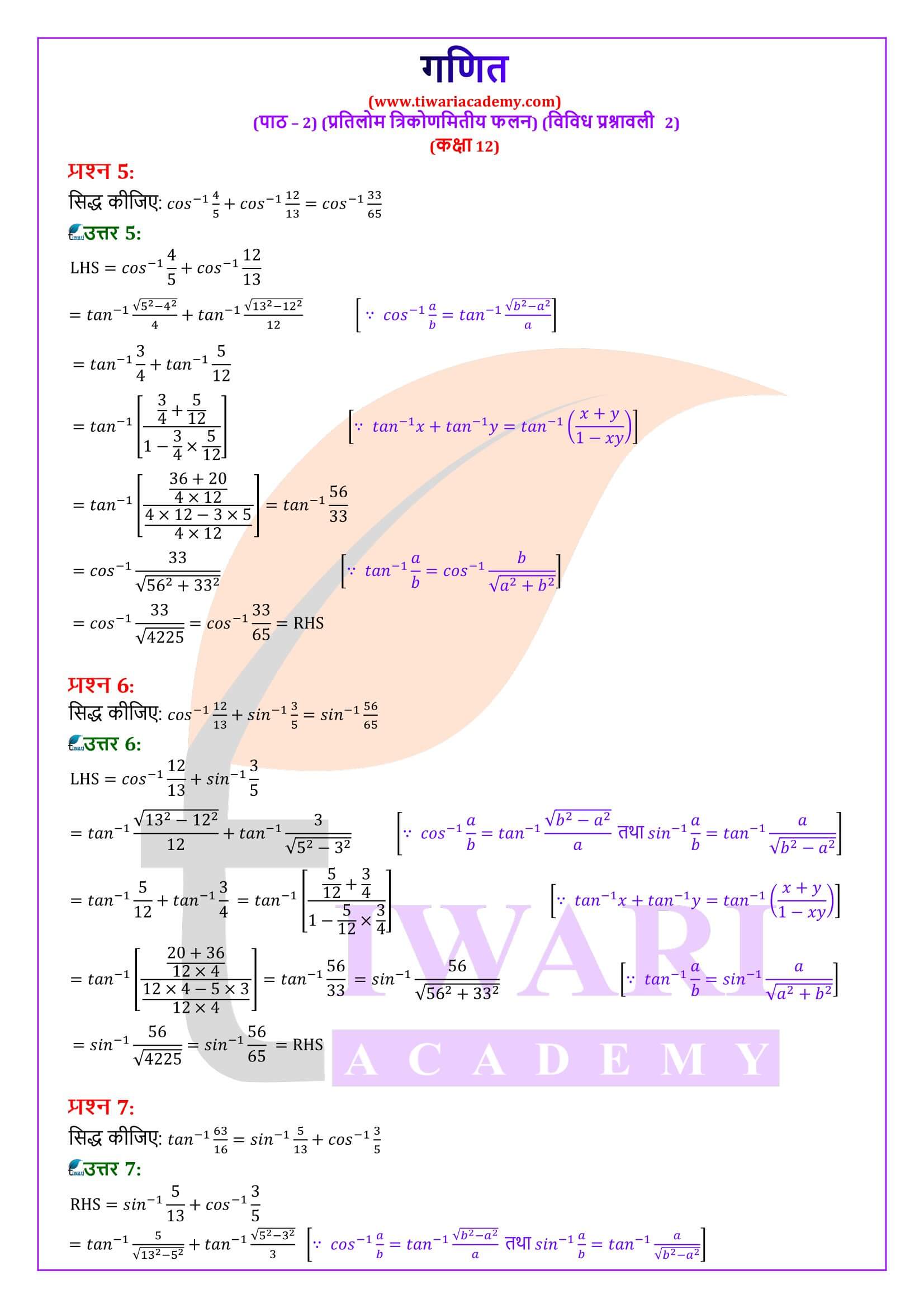
(i) sin⁻¹ x + cos⁻¹ x = π/2, x ∈ [-1, 1]
(ii) tan⁻¹ x + cot⁻¹ x = π/2, x ∈ R
(iii) cosec⁻¹ x + sec⁻¹ x = π/2, ।x। ≥ 1
पहले परिणाम को सिद्ध करने के लिए हम sin⁻¹ x = y मान लेते हैं, अर्थात, sin y = x = cos (π/2 – y)
इसलिए cos⁻¹ x = (π/2 – y) = π/2 – sin⁻¹ x
अतः sin⁻¹ x + cos⁻¹ x = π/2
sin⁻¹ 1/x = cosec⁻¹ x
इसी प्रकार अन्य भागों को भी सिद्ध कर सकते हैं।
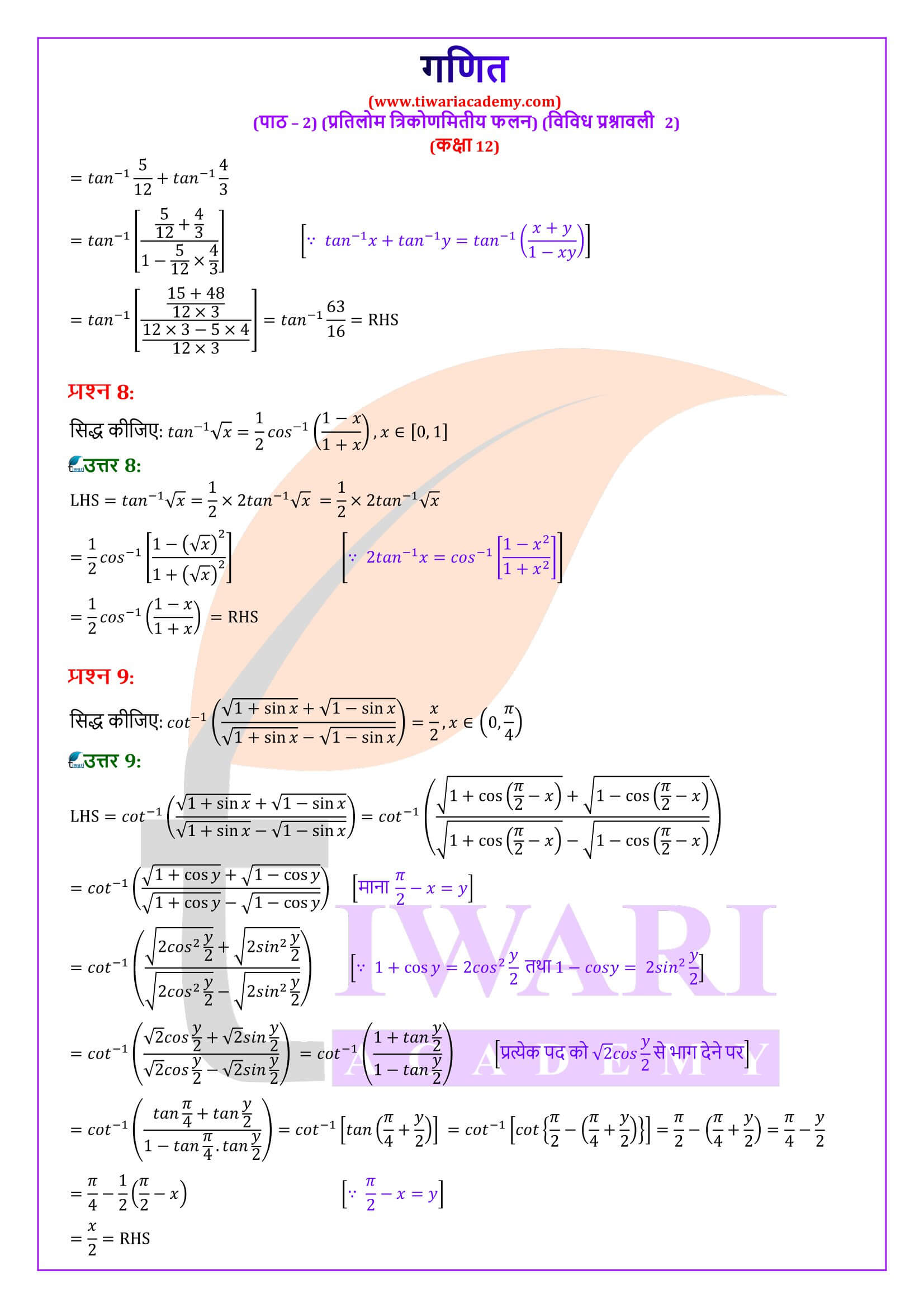
प्रतिलोम फलनों के लिए नियम
(i) tan⁻¹ x + tan⁻¹ y = tan⁻¹ (x + y)/(1 – xy), xy < 1
(ii) tan⁻¹ x - tan⁻¹ y = tan⁻¹ (x - y)/ (1 + xy), xy > -1
(iii) tan⁻¹ x + tan⁻¹ y = π + tan⁻¹ (x + y)/ (1 – xy), xy > 1, x > 0, y > 0
पहले परिणाम को सिद्ध करने के लिए मान लीजिये कि tan⁻¹ x = θ और tan⁻¹ y = ∅
तो x = tan θ तथा y = tan ∅
अब tan (θ + ∅) = (tan θ + tan ∅)/ (1 – tan θtan ∅) = (x + y)/(1 – xy)
अतः (θ + ∅) = tan⁻¹ (x + y)/(1 – xy)
इस प्रकार, tan⁻¹ x + tan⁻¹ y = tan⁻¹ (x + y)/(1 – xy),
उपर्युक्त परिणाम में यदि y को –y प्रतिस्थापित करें तो हमें दूसरा परिणाम प्राप्त होता है और y को x से प्रतिस्थापित करने से तीसरा परिणाम परिणाम प्राप्त होता है।
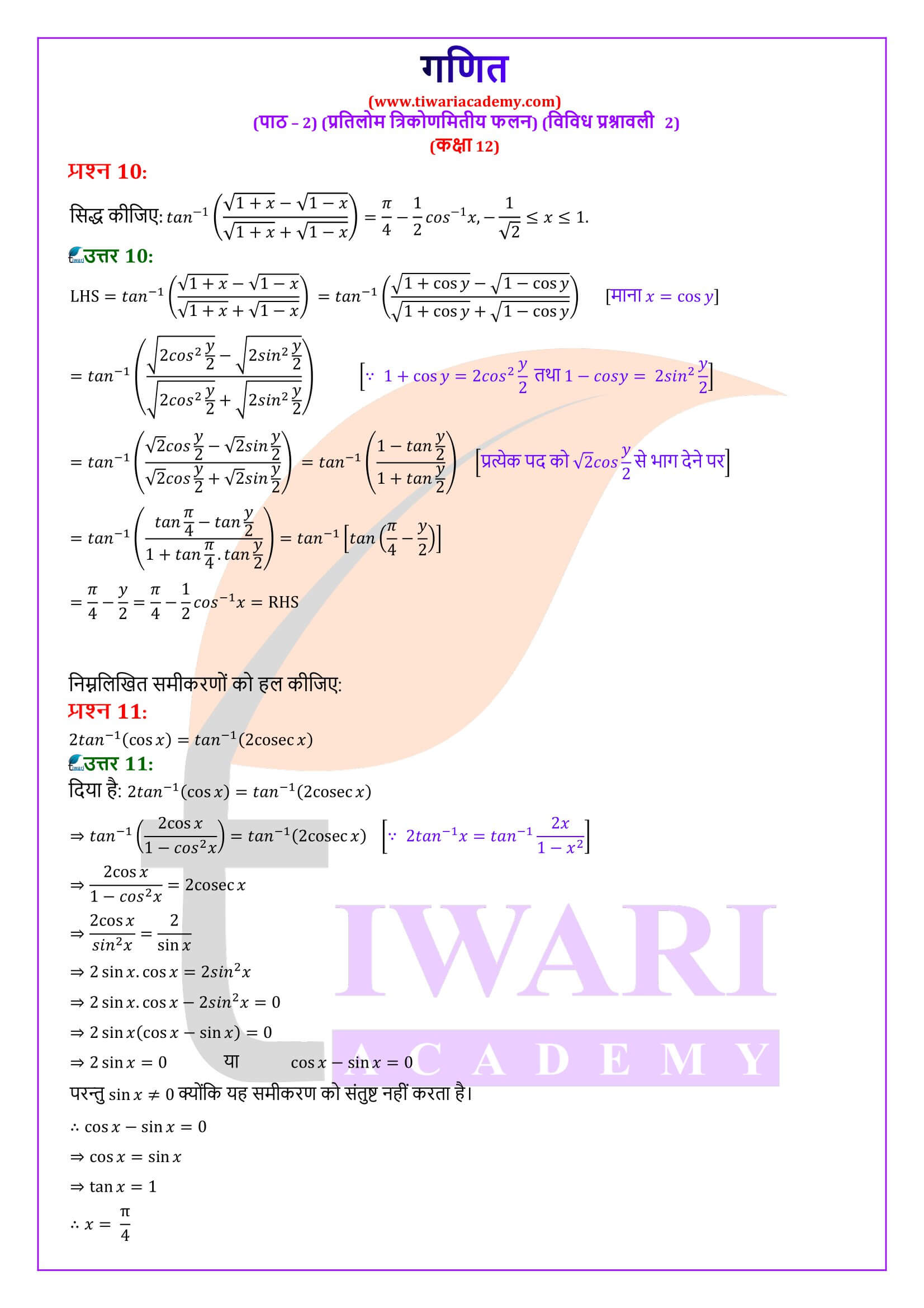
प्रतिलोम त्रिकोणमितीय फलन मुख्य गुणधर्म
(i) 2tan⁻¹ x = sin⁻¹ 2x / (1 + x²), ।x। ≤ 1
(ii) 2tan⁻¹ x = cos⁻¹ (1 – x²) / (1 + x²), x ≥ 0
(iii) 2tan⁻¹ x = tan⁻¹ 2x / (1 – x²), -1< x < 1
मान लीजिये कि tan⁻¹ x = y, तो x = tan y
अब, sin⁻¹ 2x /(1 + x²) = 2tan y / (1 + tan² y)
= sin⁻¹ (sin 2y) = 2y = 2tan⁻¹ x
इसी प्रकार हम शेष दो भागों को भी सिद्ध कर सकते हैं।