एनसीईआरटी समाधान कक्षा 8 गणित प्रश्नावली 6.1

घन एक ऐसी ठोस आकृति है, जिसकी सभी भुजाएँ बराबर होती हैं। शब्द ‘घन’ का प्रयोग ज्यामिति में किया जाता है। यहाँ पर घन संख्याओं और उनके घनमूल के बारे में अध्ययन करेंगे।
संख्याओं 1, 8, 27, — पर विचार कीजिए, ये पूर्ण घन या घन संख्याएँ कहलाती हैं। क्या आप बता सकते हैं कि इनको ये नाम क्यों दिए गए हैं? इनमें से प्रत्येक संख्या तब प्राप्त होती है, जब एक संख्या को तीन बार लेकर गुणा किया जाता है।
हम देखते हैं कि 1 = 1 × 1 × 1 = 1³
8 = 2 × 2 × 2 = 2³
27 = 3 × 3 × 3 = 3³ है।

क्रमागत विषम संख्याओं को जोड़ना विषम संख्याओं के योगों के निम्नलिखित प्रतिरूप को देखिए:
1 = 1 = 1³
3 + 5 = 8 = 2³
7 + 9 + 11 = 27 = 3³
13 + 15 + 17 + 19 = 64 = 4³
21 + 23 + 25 + 27 + 29 = 125 = 5³

कुछ संख्याओं और उनके घनों के निम्नलिखित अभाज्य गुणनखंडनों पर विचार कीजिए:
एक संख्या का अभाज्य गुणनखंडन उसके घन का अभाज्य गुणनखंडन
4 = 2 × 2 4³ = 64 = 2 × 2 × 2 × 2 × 2 × 2 = 2³ × 2³
6 = 2 × 3 6³ = 216 = 2 × 2 × 2 × 3 × 3 × 3 = 2³ × 3³
15 = 3 × 5 15³ = 3375 = 3 × 3 × 3 × 5 × 5 × 5 = 3³ × 5³
12 = 2 × 2 × 3 12³ = 1728 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3 = 2³ × 2³ × 3³
ध्यान दीजिए कि एक संख्या का प्रत्येक अभाज्य गुणनखंड उस संख्या के घन के अभाज्य गुणनखंडन् में तीन बार आता है।

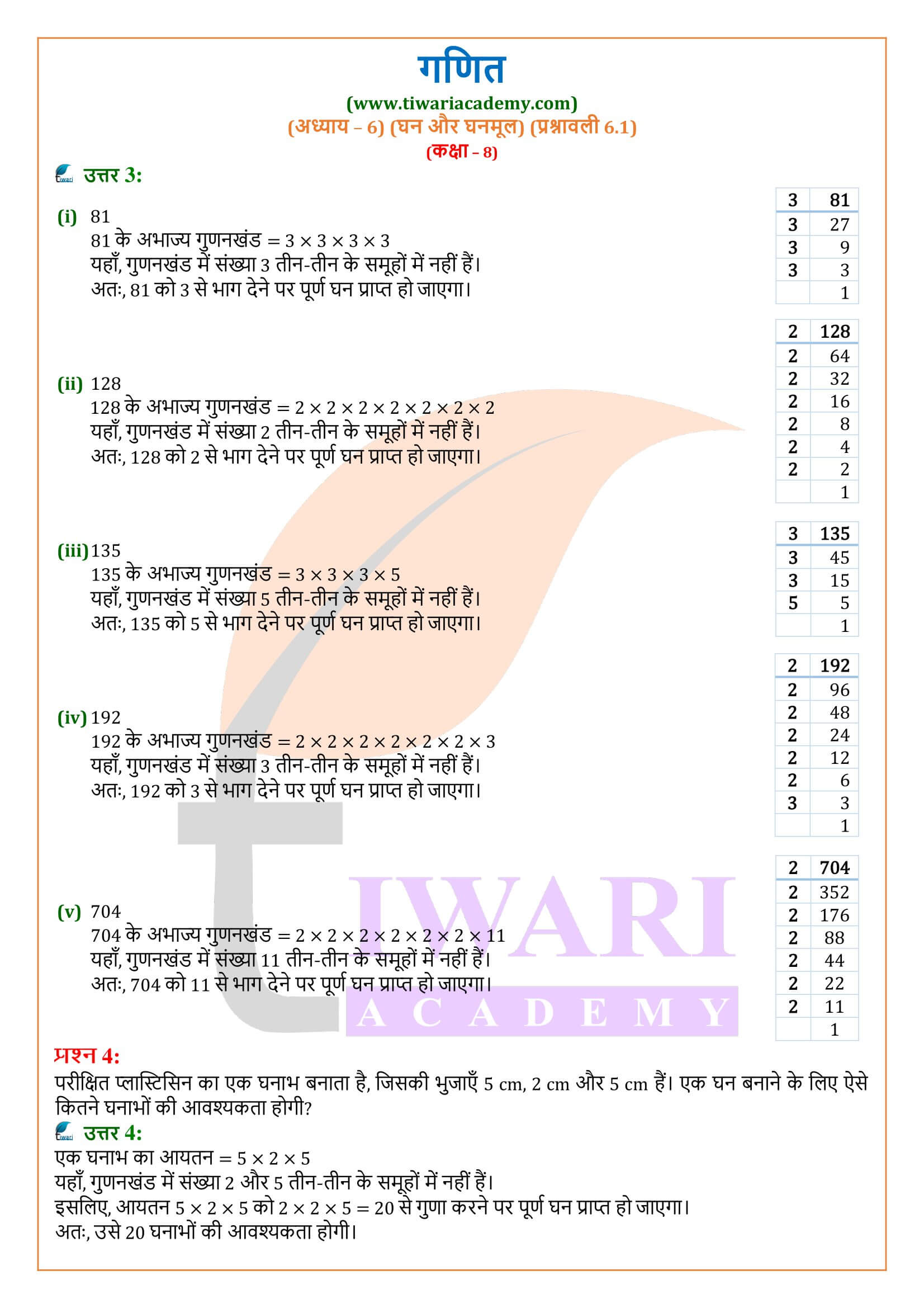
क्या 243 एक पूर्ण घन है?
हल:
243 = 3 × 3 × 3 × 3 × 3
यहाँ 3 का एक त्रिक बनाने के बाद 3 × 3 शेष रहता है। अतः, 243 एक पूर्ण घन नहीं है।
सबसे छोटा गुणज जो पूर्ण घन है।

राज ने प्लास्टिसिन का एक घनाभ बनाया। इस घनाभ की लंबाई, चौड़ाई और ऊँचाई क्रमशः 15 बउए 30 बउ और 15 बउ है। अनु उससे पूछती है कि एक (पूर्ण) घन बनाने के लिए उसे ऐसे कितने घनाभों की आवश्यकता होगी? क्या आप बता सकते हैं?
राज कहता है,
घनाभ का आयतन = 15 × 30 × 15
= 3 × 5 × 2 × 3 × 5 × 3 × 5
= 2 × 3 × 3 × 3 × 5 × 5 × 5
क्योंकि उपरोक्त अभाज्य गुणनखंडन में केवल एक बार 2 है, इसलिए हमें इसे पूर्ण घन बनाने के लिए 2 × 2 = 4 की आवश्यकता होगी।
अतः हमें एक घन बनाने के लिए ऐसे चार घनाभों की आवश्यकता होगी।