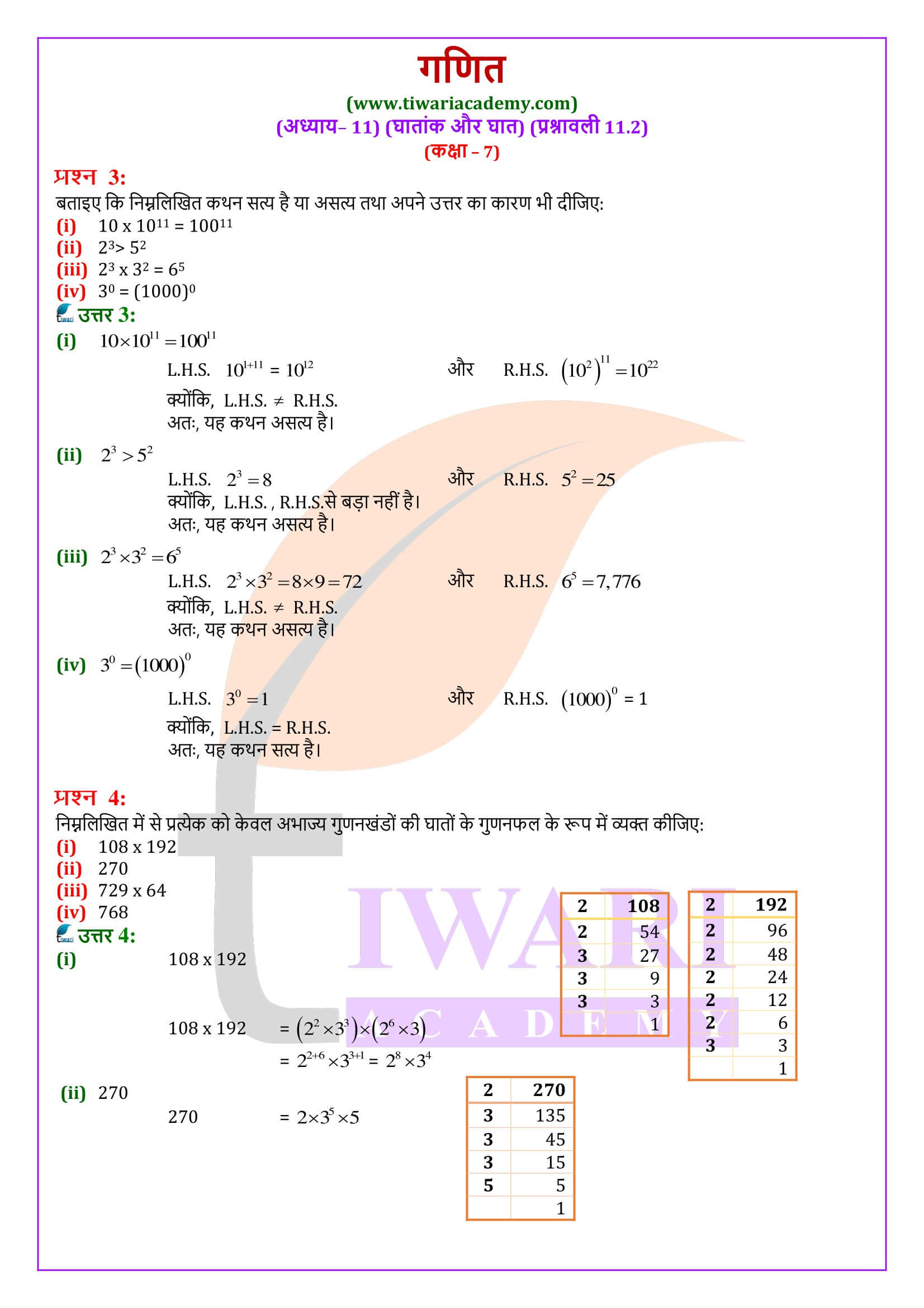
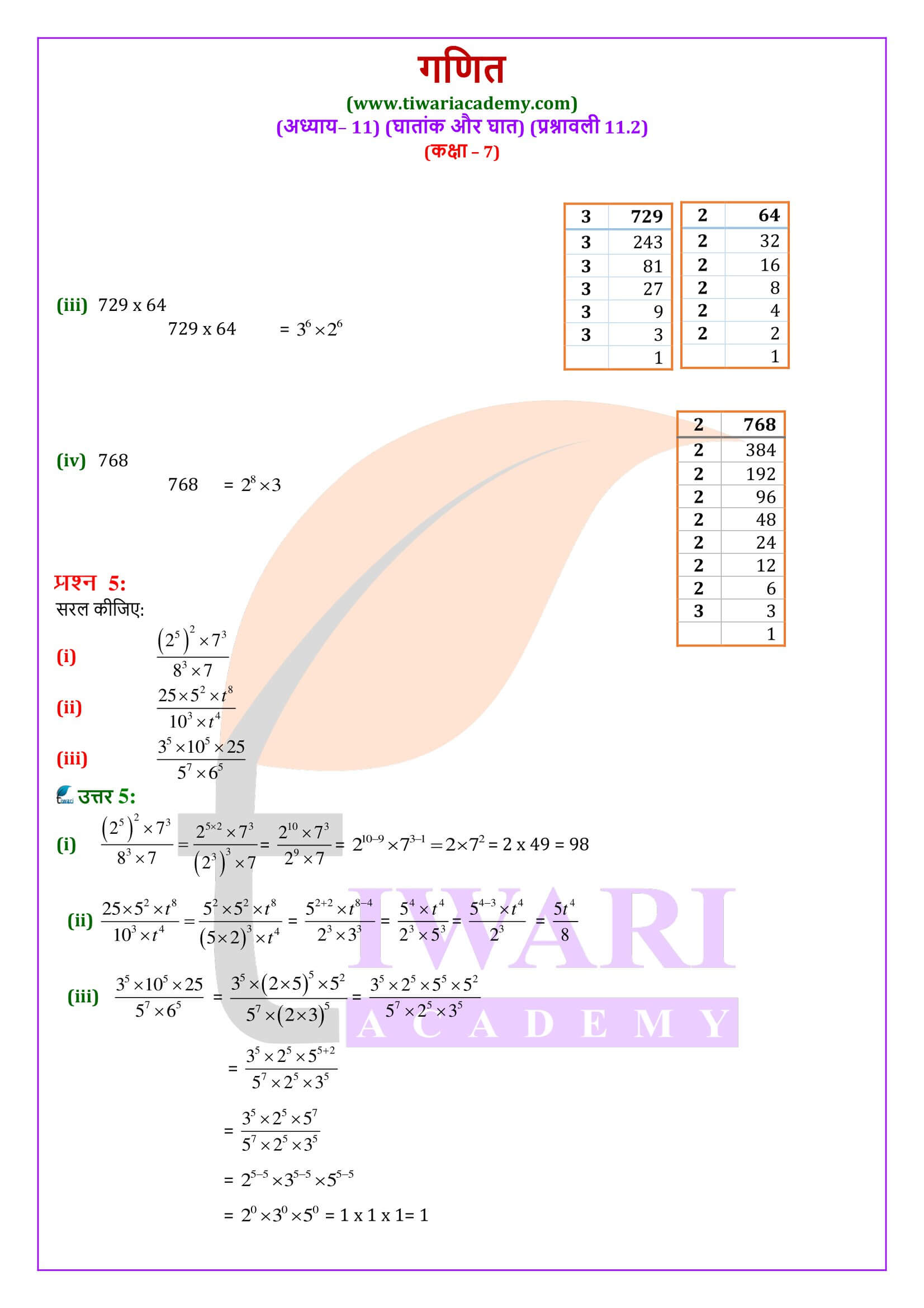
एनसीईआरटी समाधान कक्षा 7 गणित प्रश्नावली 11.2

घातांकों के गुणन, विभाजन तथा घात की घात को कैसे हल किया जाता है इसके कुछ नियम हैं जो निम्नलिखित हैं:
एक ही आधार वाली घातों का गुणन
(i) आइए 2² × 2³ को परिकलित करें।
2² × 2³ = (2 × 2) × (2 × 2 × 2)
= 2 × 2 × 2 × 2 × 2 = 2⁵ = 2²⁺³
ध्यान दीजिए कि 2² और 2³ में आधार एक ही (समान) है तथा घातांकों का योग, अर्थात् 2 और 3 का योग 5 है।

(ii) (–3)⁴ × (–3)³ = [(–3) × (–3) × (–3)× (–3)] × [(–3) × (–3) × (–3)]
= (–3) × (–3) × (–3) × (–3) × (–3) × (–3) × (–3)
= (–3)⁷
= (–3)⁴⁺³
पुनः ध्यान दीजिए कि आधार एक ही है तथा घातांकों का योग 4 + 3 = 7 है।
यहाँ से हम व्यापक रूप से यह कह सकते हैं कि एक शून्येतर पूर्णांक a, के लिए, aᵐ × aⁿ = aᵐ⁺ⁿ होता है, जहाँ m और n पूर्ण संख्याएँ हैं।

किसी भी शून्येतर पूर्णांक a के लिए, aᵐ ÷ aⁿ = aᵐ ⁻ ⁿ होता है, जहाँ m और n पूर्ण संख्याएँ हैं तथा m > n है।
उदाहरण:
आइए 3⁷ ÷ 3⁴ को सरल करें।
3⁷ ÷ 3⁴ = 3⁷ / 3⁴ = (3 × 3 × 3 × 3 × 3 × 3 × 3)/( 3 × 3 × 3 × 3)
= 3 × 3 × 3
= 3⁷ ⁻ ⁴ = 3³
ध्यान दीजिए कि 3⁷ और 3⁴ के आधार एक ही हैं और 3⁷ > 3⁴ = 3⁷ ⁻ ⁴ हो जाता है।

किसी शून्येतर पूर्णांक a के लिए, (aᵐ)ⁿ = aᵐⁿ होता है, जहाँ m और n पूर्ण संख्याएँ हैं।
उदाहरण:
क्या आप बता सकते हैं कि (5²) × 3 और (5²)³ में से कौन बड़ा है?
हल:
(5²) × 3 का अर्थ है कि 5² को 3 से गुणा किया गया है, अर्थात् यह 5 × 5 × 3 = 75
परंतु (5²)³ का अर्थ है कि 5² का स्वयं से तीन बार गुणा किया गया है, अर्थात् यह 5² × 5² × 5²
= 5⁶ = 15625 है।
अतः, (5²)³ > (5²) × 3 है।

किसी भी शून्येतर पूर्णांक के लिए, aᵐ × bᵐ = (ab)ᵐ होता है जहाँ, m एक पूर्ण संख्या है।
उदाहरण:
निम्नलिखत पदों को घातांकीय रूप में व्यक्त कीजिए:
(i) (2 × 3)⁵
(ii) (2a)⁴

हल:
(i) (2 × 3)⁵ = (2 × 3) × (2 × 3) × (2 × 3) × (2 × 3) × (2 × 3)
= (2 × 2 × 2 × 2 × 2) × (3 × 3× 3 × 3 × 3)
= 2⁵ × 3⁵
(ii) (2a)⁴ = 2a × 2a × 2a × 2a
= (2 × 2 × 2 × 2) × (a × a × a × a)
= 2⁴ × a⁴