एनसीईआरटी समाधान कक्षा 11 गणित प्रश्नावली 9.1
एनसीईआरटी समाधान कक्षा 11 गणित प्रश्नावली 9.1 सरल रेखाएँ अभ्यास के प्रश्नों के हल सीबीएसई और राजकीय बोर्ड के विद्यार्थियों के लिए सत्र 2025-26 के अनुसार यहाँ दिए गए हैं। कक्षा 11 गणित के छात्र प्रश्नावली 9.1 के सवाल जवाब यहाँ दी गई पीडीएफ और विडियो के माध्यम से भी आसानी से समझ सकते हैं।
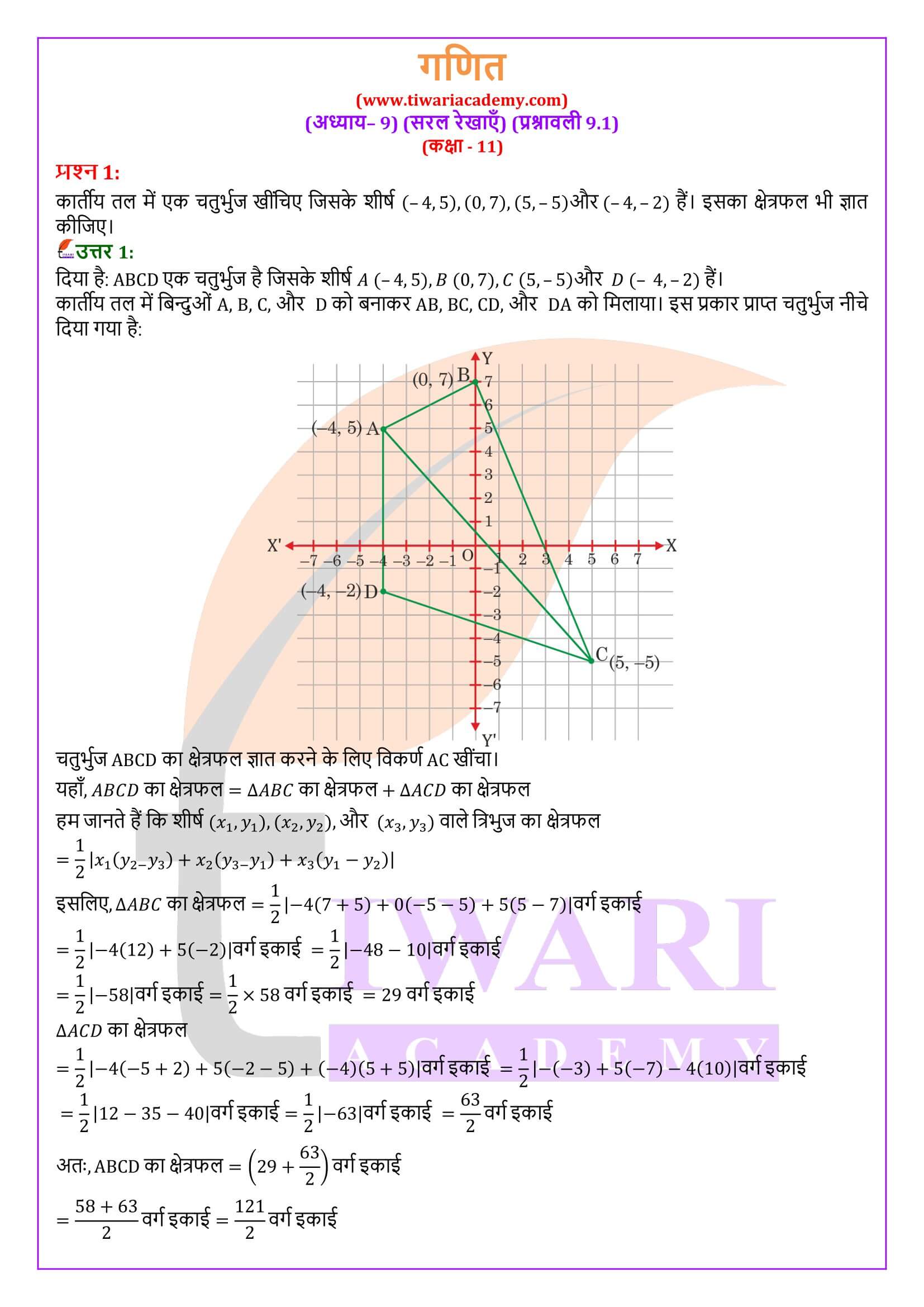
एनसीईआरटी समाधान कक्षा 11 गणित प्रश्नावली 9.1
कक्षा 11 गणित प्रश्नावली 9.1 के लिए एनसीईआरटी समाधान
सरल रेखा
सरल रेखा गणित में शून्य चौड़ाई वाला अनन्त लम्बाई वाला एक आदर्श वक्र होता है, यूक्लिडीय ज्यामिति के अन्तर्गत दो बिन्दुओं से होकर एक और केवल एक ही रेखा जा सकती है। एक सरल रेखा दो बिदुओं के बीच की लघतुत्तम दूरी प्रदर्शित करती है। सरल रेखा बिन्दुओं का सरलतम बिन्दुपथ होता है।
सरल रेखा सम्बन्धी कुछ महत्वपूर्ण सूत्र
1. P (x₁, y₁) और Q (x₂, y₂) बिंदुओं के बीच की दूरी
PQ = √{(x₂ – x₁)² + (y₂ – y₁)²} है।
उदाहरणार्थ, (6, -4) और (3, 0) बिंदुओं के बीच की दूरी
= √{(3 – 6)² + (0 + 4)²} = 5 इकाई है।
2. P (x₁, y₁) और Q (x₂, y₂) बिंदुओं को मिलाने वाले रेखाखंड को m: n में अंतःविभाजित करने वाले बिंदु के निर्देशांक
{(mx₂ + nx₁)/(m + n), (my₂ + ny₁)/(m + n)}
उदाहरणार्थ, उस बिंदु के निर्देशांक जो A (1, -3) और B (-3, 9) को मिलाने वाले रेखाखंड को 1: 3 में अंतःविभाजित करता है, इसलिए
x = {(1 × -3 + 3 × 1)/(1 + 3) = 0
y = (1 × 9 + 3 × -3)/(1 + 3)} = 0
अतः बिंदु (x, y) के निर्देशांक (0, 0) हैं।
3. विशेष रूप में यदि m = n, तो (x₁, y₁) और (x₂, y₂) बिंदुओं को मिलाने वाले रेखाखंड के मध्य बिंदु के निर्देशांक
{(x₂ + x₁)/2, (y₂ + y₁)/2} हैं।
4. (x₁, y₁), (x₂, y₂) और (x₃, y₃) शीर्षों से बने त्रिभुज का क्षेत्रफल
= ½[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)} वर्ग इकाई है।
उदाहरणार्थ, एक त्रिभुज जिसके शीर्ष (4, 4), (3, -2) और (-3, 16) हैं,
उसका क्षेत्रफल = ½[4(-2 – 16) + 3(16 – 4) – 3(4 – 2)] = I-54I/2 = 27 वर्ग इकाई है।
याद रखने योग्य बातें
यदि त्रिभुज ABC का क्षेत्रफल शून्य है, तो तीन बिंदु A, B और C एक रेखा पर होते हैं अर्थात् वे स्ंरेख हैं।
रेखा की ढाल
यदि θ¬ किसी रेखा l का झुकाव है, तो tan θ को रेखा l की ढाल कहते हैं।
निर्देशांक तल में एक रेखा x-अक्ष, के साथ दो कोण बनाती है, जो परस्पर संपूरक होते हैं। कोण θ (मान लीजिए) जो रेखा l, x-अक्ष की धनात्मक दिशा के साथ बनाती है, रेखा l का झुकाव कहलाता है। स्पष्टतया 0° ≤ θ < 180°
नोट:
वह रेखा जिसका झुकाव 90° है, उसकी ढाल परिभाषित नहीं है। एक रेखा की ढाल को m से व्यक्त करते हैं। इस प्रकार m = tan θ, ¬ θ ≠ 90° यह देखा जा सकता है कि x अक्ष की ढाल शून्य है और y अक्ष की ढाल परिभाषित नहीं है।