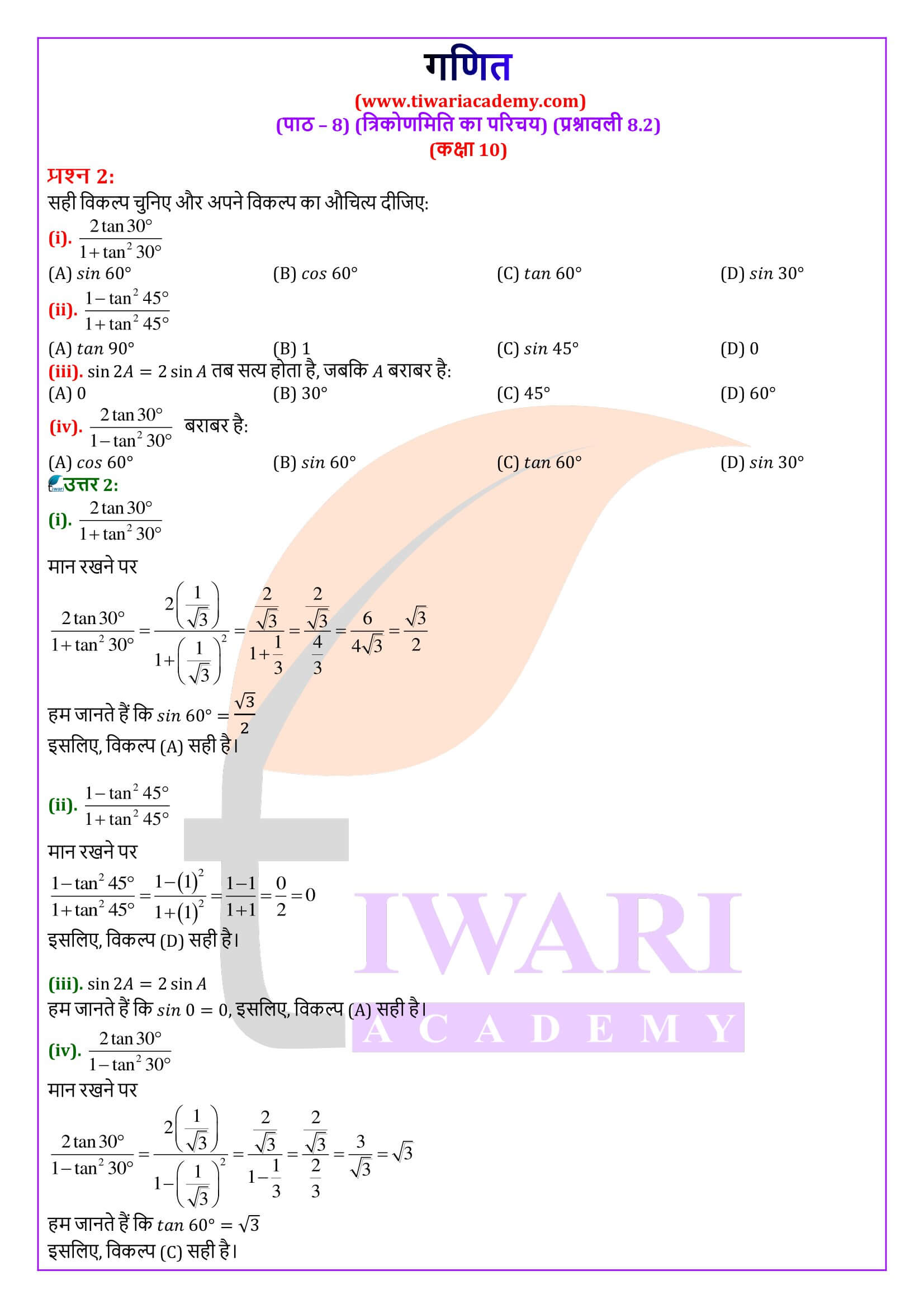
एनसीईआरटी समाधान कक्षा 10 गणित प्रश्नावली 8.2

ज्यामिति के अध्ययन से आप 30°, 45°, 60° और 90° के कोणों की रचना से आप अच्छी तरह से परिचित हैं। इस अनुच्छेद में हम इन कोणों और साथ ही 0° वाले कोण के त्रिकोणमितीय अनुपातों के मान ज्ञात करेंगे।

∆ ABC में, जिसका कोण B समकोण है, यदि एक कोण 45° का हो, तो अन्य कोण भी 45° का होगा अर्थात्
∠ A = ∠ C = 45°
अतः BC = AB
मान लीजिये BC = AB = a
तब पाइथागोरस प्रमेय के अनुसार AC² = AB² + BC² = a² + a² = 2a²
⟹ AC = a√2

त्रिकोणमितीय अनुपातों की परिभाषाओं को लागू करने पर हमें यह प्राप्त होता है:
sin 45° = BC/AC = a/a√2 = 1/√2
cos 45° = AB/AC = a/a√2 = 1/√2
tan 45° = BC/AB = a/a = 1
cot 45° = AB/BC = a/a = 1
cosec 45° = AC/BC = a√2/a = √2
sec 45° = AC/AB = a√2/a = √2

अब हम 30° और 60° के त्रिकोणमितीय अनुपात परिकलित करें। एक समबाहु त्रिभुज ABC पर विचार करें। क्योंकि समबाहु त्रिभुज का प्रत्येक कोण, 60° का होता है, इसलिए ∠A = ∠B = ∠C = 60°
A से भुजा BC पर लंब AD डालिए
अब ∆ ABD ≅ ∆ ACD (क्यों?)
इसलिए, BD = DC
और ∠ BAD = ∠ CAD (CPCT)

अब आप यह देख सकते हैं किः
∆ ABD एक समकोण त्रिभुज है जिसका कोण D समकोण है, और जहाँ ∠ BAD = 30° और ∠ ABD = 60°
त्रिकोणमितीय अनुपातों को ज्ञात करने के लिए हमें त्रिभुज की भुजाओं की लंबाइयाँ ज्ञात करने की आवश्यकता होती है। आइए, हम यह मान लें कि AB = 2a
तब BD = ½ BC = a
और AD² = AB² – BD² = (2a)² – (a)² = 3a²

इसलिए, AD = a√3
अब sin 30° = BD/AB = a/2a = 1/2
cos 30° = AD/AB = a√3/2a = √3/2
tan 30° = BD/AD = a/a√3 = 1/√3
cot 30° = BD/AB = a√3/a = √3
cosec 30° = AB/BD = 2a/a = 2
sec 30° = BD/AB = 2a/a√3 = 2/√3

इसी प्रकार
sin 60° = AD/AB = a√3/2a = √3/2
cos 60° = 1/2
tan 60° = √3
cot 60° = 1/√3
cosec 60° = 2/√3
sec 60° = 2