एनसीईआरटी समाधान कक्षा 10 गणित प्रश्नावली 5.2
एनसीईआरटी समाधान कक्षा 10 गणित अध्याय 5 प्रश्नावली 5.2 समांतर श्रेढियाँ के हल हिंदी में सीबीएसई तथा राजकीय बोर्ड के लिए सत्र 2025-26 के अनुसार यहाँ से प्राप्त किए जा सकते हैं। ये समाधान नए शैक्षणिक सत्र के अनुसार संशोधित किए गए हैं। प्रत्येक प्रश्न को विस्तार से चरणबद्ध तरीके से समझाया गया है। पीडीएफ के साथ साथ विडियो समाधान भी दिया गया है ताकि छात्र प्रत्येक प्रश्न को आसानी से समझ सकें।
एनसीईआरटी समाधान कक्षा 10 गणित अध्याय 5 प्रश्नावली 5.2
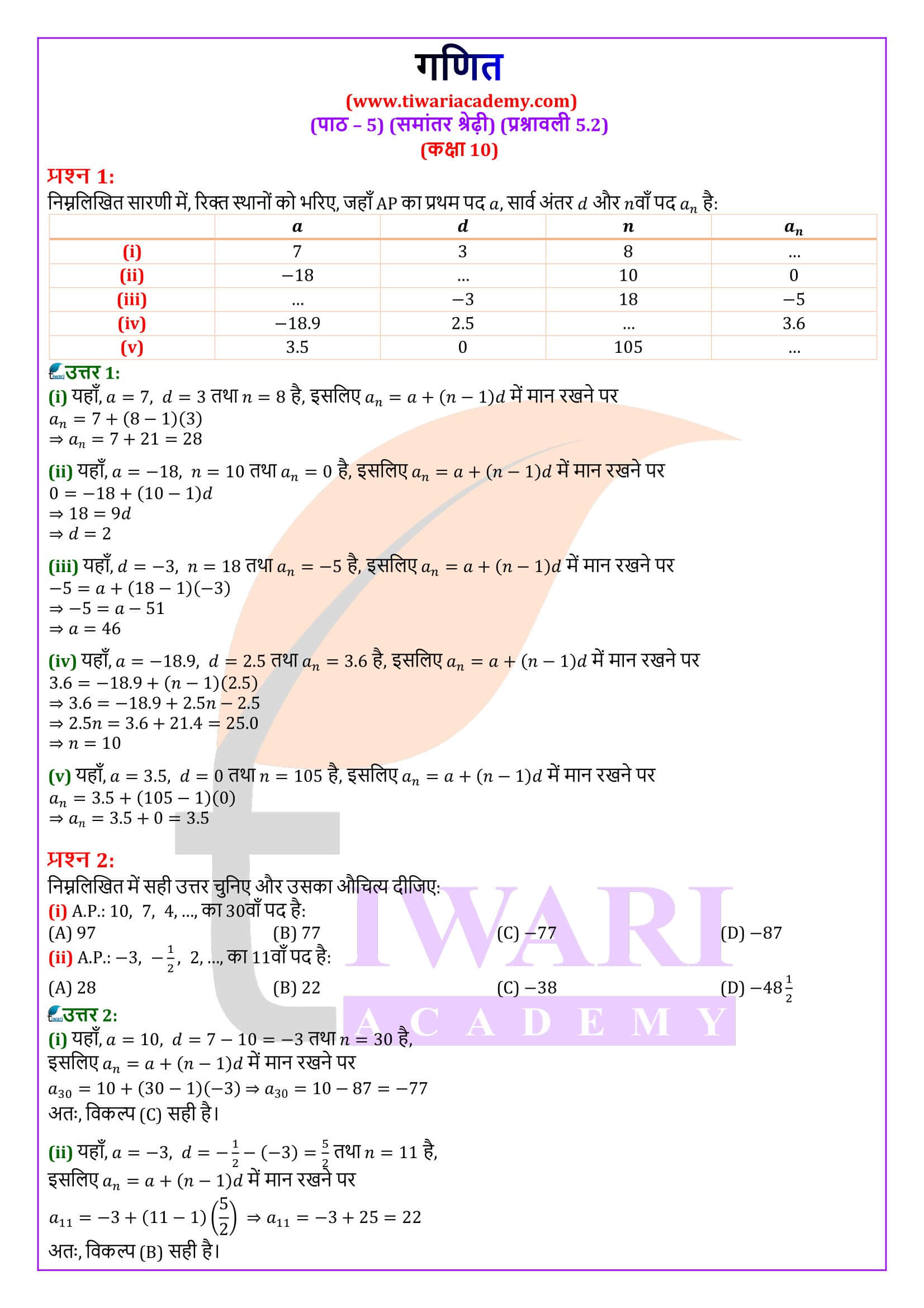
कक्षा 10 गणित अध्याय 5 प्रश्नावली 5.2 के लिए एनसीईआरटी समाधान
समांतर श्रेढ़ी के प्रकार
समांतर श्रेढ़ी को मुख्यतः दो प्रकार से परिभाषित किया जाता है:
- परिमित समान्तर श्रेढ़ी
- अपरिमित समान्तर श्रेढ़ी
परिमित समान्तर श्रेढ़ी
एक समान्तर श्रेढ़ी जिसमें संख्याएँ सीमित होती हैं उसे परिमित समान्तर श्रेढ़ी कहते हैं। इस प्रकार की समान्तर श्रेढ़ी में अंतिम पद होता है।
उदाहरण – 5, 10, 15, 20, 25, 30 ………………………….100 (अंतिम पद)।
अपरिमित समान्तर श्रेढ़ी
एक समान्तर श्रेढ़ी जिसमें अनंत संख्या में पद होते हैं उसे अपरिमित समान्तर श्रेढ़ी कहा जाता है। इस प्रकार की समान्तर श्रेढ़ी में अंतिम पद नहीं होता है।
उदाहरण: 10, 20, 30, 40, 50, 60 …………………………….. एक समांतर श्रेढ़ी है।
समान्तर श्रेढ़ी का n वाँ पद (व्यापक पद)
हमें समान्तर श्रेढ़ी का व्यापक रूप पता हैं जो कि इस तरह लिखा जाता है।
a, a + d, a + 2d, a + 3d, a + 4d, …………….., a + (n – 1) d
यहाँ, पहला पद a है। दूसरा पद ज्ञात करने के लिए पहले पद a में सार्व अंतर d जोड़ते हैं या हम कह सकते हैं कि सार्व अंतर d को (2 – 1) से गुणा कर रहे हैं और फिर पहले पद a में जोड़ रहे हैं।
a₂ = a + d = a + (2 – 1) d
तीसरा पद ज्ञात करने के लिए, उपरोक्त अनुसार हम सार्व अंतर d को (3 – 1) से गुणा कर रहे हैं और पहले पद a में जोड़ रहे हैं।
a₃ = a + 2d = a + (3 – 1) d
इसी तरह, समान्तर श्रेढ़ी का n वाँ पद ज्ञात करने के लिए सार्व अंतर d को (n – 1) से गुणा करेंगे और फिर पहले पद a में जोड़ेंगे जैसा व्यापक रूप में भी लिखा गया है।
aₙ = a + (n – 1) d
यहाँ, aₙ = n वाँ पद या इसको व्यापक पद भी कहते हैं।
यदि किसी समान्तर श्रेढ़ी में m पद हैं, तो aₘ इसके अंतिम पद को निरूपित करता है, जिसे कभी-कभी l द्वारा भी व्यक्त किया जाता है।
अभ्यास के लिए प्रश्न
2, 7, 12, ………… का 10वाँ पद ज्ञात कीजिए।
उत्तर:
यहाँ पर a₁ = 2, a₂ = 7
इसलिए, d = a₂ – a₁ = 7 – 2 = 5
क्योंकि aₙ = a + (n – 1) d
इसलिए, 10वां पद
a₁₀ = a₁ + (10 – 1) d
= 2 + 9 × 5 = 47
अतः 10वां पद है।
अतिरिक्त प्रश्नों के हल
21, 18, 15, ………… का कौन-सा पद – 81 है? साथ ही क्या इस A. P. का कोई पद शून्य है? सकारण उत्तर दीजिए।
उत्तर:
यहाँ, a = 21, d = 18 – 21 = – 3 और aₙ = – 81 है। हमें n ज्ञात करना है।
चूँकि aₙ = a + (n – 1) d
अतः – 81 = 21 + (n – 1)(- 3)
या – 81 = 24 – 3n
या – 105 = – 3n
अतः n = 35
इसलिए, दी हुई A. P. का 35वाँ पद – 81 है।
आगे, हम यह जानना चाहते हैं कि क्या कोई n ऐसा है कि aₙ = 0 हो। यदि ऐसा कोई n
है तो
21 + (n – 1) (-3) = 0
अर्थात् 3(n – 1) = 21
या n = 8
अतः 8वां पद 0 है।
वह A. P. निर्धारित कीजिए जिसका तीसरा पद 5 और 7वाँ पद 9 है।
हमें प्राप्त है
a₃ = a + (3 – 1) d = a + 2d = 5 (1)
और
a₇ = a + (7 – 1) d = a + 6d = 9 (2)
समीकरणों (1) और (2) के युग्म को हल करने पर, हमें प्राप्त होता है:
a = 3, d = 1
अतः वांछित A. P.: 3, 4, 5, 6, 7, ………. है।