एनसीईआरटी समाधान कक्षा 7 गणित प्रश्नावली 11.1
एनसीईआरटी समाधान कक्षा 7 गणित प्रश्नावली 11.1 घातांक और घात के हल हिंदी और अंग्रेजी में सवाल जवाब शैक्षणिक सत्र 2025-26 के लिए यहाँ से निशुल्क प्राप्त करें। कक्षा 7 गणित के छात्र अध्याय 11.1 के प्रश्नों के हल के लिए यहाँ दिए गए पीडीएफ समाधान की मदद ले कर प्रत्येक प्रश्न को आसानी से हल कर सकते हैं।
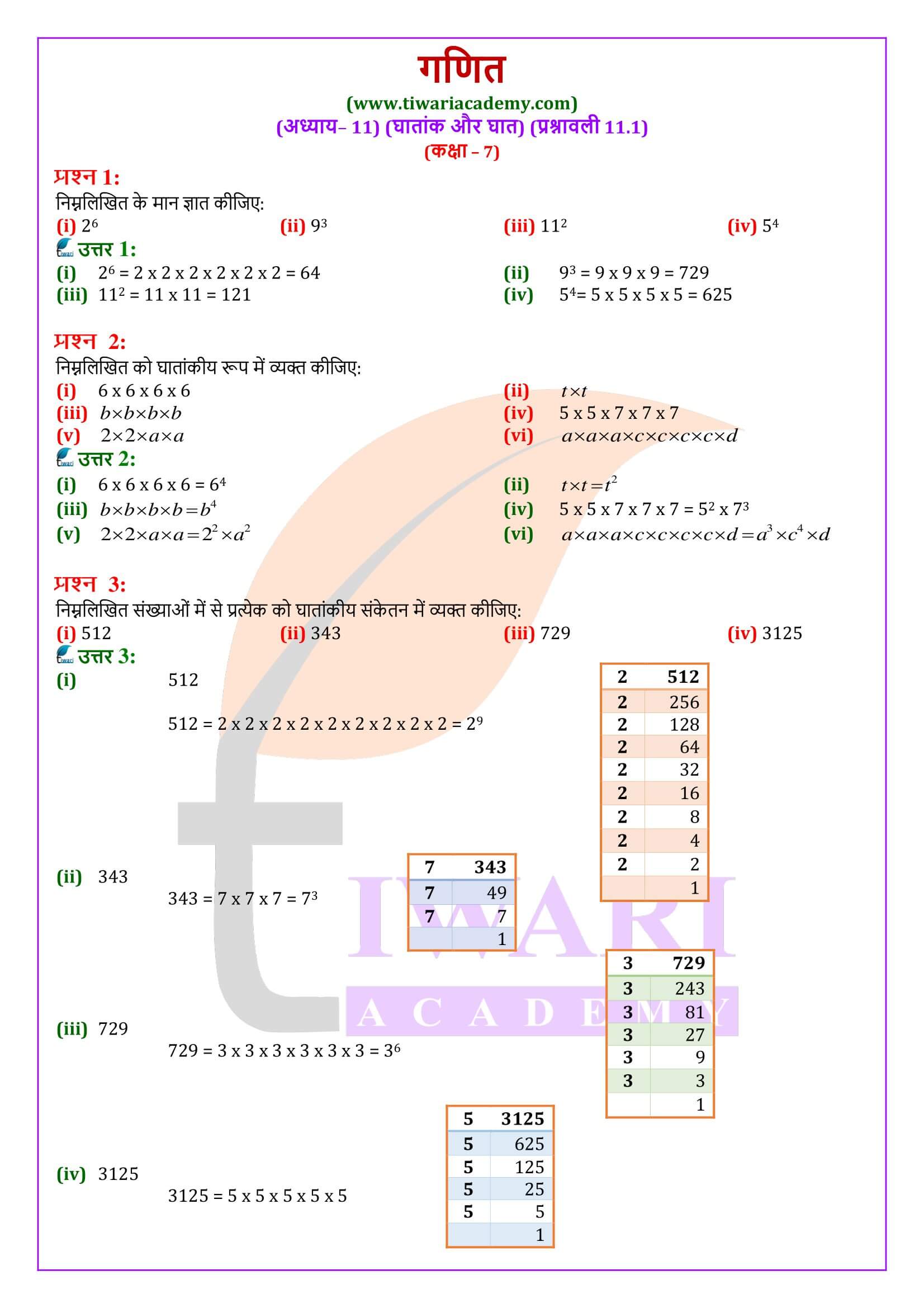
एनसीईआरटी समाधान कक्षा 7 गणित प्रश्नावली 11.1
कक्षा 7 गणित प्रश्नावली 11.1 घातांक और घात के प्रश्नों के हल
घातांक
किसी वास्तविक संख्या को उसी संख्या से जितनी बार गुणा किया जाता है तो जितनी बार गुणा किया जाता है तो उसे उस संख्या का घातांक कहते हैं।
हम बड़ी संख्याओं को घातांकों का प्रयोग करके संक्षिप्त रूप में लिख सकते हैं।
संक्षिप्त संकेतन 10⁴ गुणनफल 10 × 10 × 10 × 10 को व्यक्त करता है। यहाँ, 10 आधार और 4 घातांक कहलाता है। 10⁴ को 10 के ऊपर घात 4 या केवल 10 की चौथी घात पढ़ा जाता है। 10⁴ को 10000 का घातांकीय रूप कहा जाता है।
10 की घात के रूप में व्यक्त करना
हम इसी प्रकार 1000 को भी 10 की घात के रूप में व्यक्त कर सकते हैं। ध्यान दीजिए कि
1000 = 10 × 10 × 10 = 10³ है।
यहाँ, पुनः 10³ संख्या 1000 का घातांकीय रूप है।
इसी प्रकार, 1,00,000 = 10 × 10 × 10 × 10 × 10 = 10⁵ है।
अर्थात्, 10⁵ संख्या 1,00,000 का घातांकीय रूप है।
इन दोनों उदाहरणों में, आधार 10 है। 10³ में घातांक 3 है तथा 10⁵ में घातांक 5 है।
हम संख्याओं को विस्तारित या प्रसारित रूप में लिखने के लिए
10, 100, 1000 इत्यादि जैसी संख्याओं का प्रयोग कर चुके हैं।
उदाहरणार्थ, 47561 = 4 × 10000 + 7 × 1000 + 5 × 100 + 6 × 10 + 1 है।
इसे 4 × 10⁴ + 7 ×10³ + 5 × 10² + 6 × 10 + 1 के रूप में लिखा जा सकता है।
घातांक का आधार
किसी घात वाली संख्या में जिस संख्या को गुणा किया जाता है उसे घातांक का आधार कहा जाता है।
उदाहरण:
81 = 3 × 3 × 3 × 3 = 3⁴ के रूप में लिखा जा सकता है। यहाँ आधार 3 है और घातांक 4 है।
कुछ घातों के विशिष्ट नाम
10², जो 10 के ऊपर घात 2 है, इसे 10 का वर्ग भी पढ़ा जाता है।
10³, जो 10 के ऊपर घात 3 है, इसे 10 का घन भी पढ़ा जाता है।
क्या आप बता सकते हैं कि 5³ (5 के घन) का क्या अर्थ है?
53 = 5 × 5 × 5 = 125
अतः हम कह सकते हैं कि 125 संख्या 5 की तीसरी घात है।
सम और विषम घात
किसी घातांक संख्या में आधार संख्या अगर धनात्मक है तो घात के सम और विषम होने से संख्यात्मक मान के अतिरिक्त कोई परिवर्तन नहीं होता है। लेकिन अगर आधार संख्या ऋणात्मक है तो घात के सम होने पर परिणाम धनात्मक होता है और अगर घात विषम है तो परिणाम ऋणात्मक होता है।
उदाहरण:
- (i) (–10)³ = (–10) × (–10) × (–10) = 100 × (–10) = – 1000
- (ii) (–5)⁴ = (–5) × (–5) × (–5) × (–5) = 25 × 25 = 625