एनसीईआरटी समाधान कक्षा 7 गणित प्रश्नावली 4.1
एनसीईआरटी समाधान कक्षा 7 गणित प्रश्नावली 4.1 सरल समीकरण के सभी सवाल जवाब हिंदी और अंग्रेजी में प्रश्नों के हल सत्र 2025-26 के लिए यहाँ दिए गए हैं। कक्षा 7 गणित अध्याय 4.1 के प्रश्न उत्तर जिन छात्रों को पीडीएफ के माध्यम से समझने में परेशानी हो वे यहाँ दिए गए विडियो समाधान की मदद लेकर इसे आसानी से समझ सकते हैं।
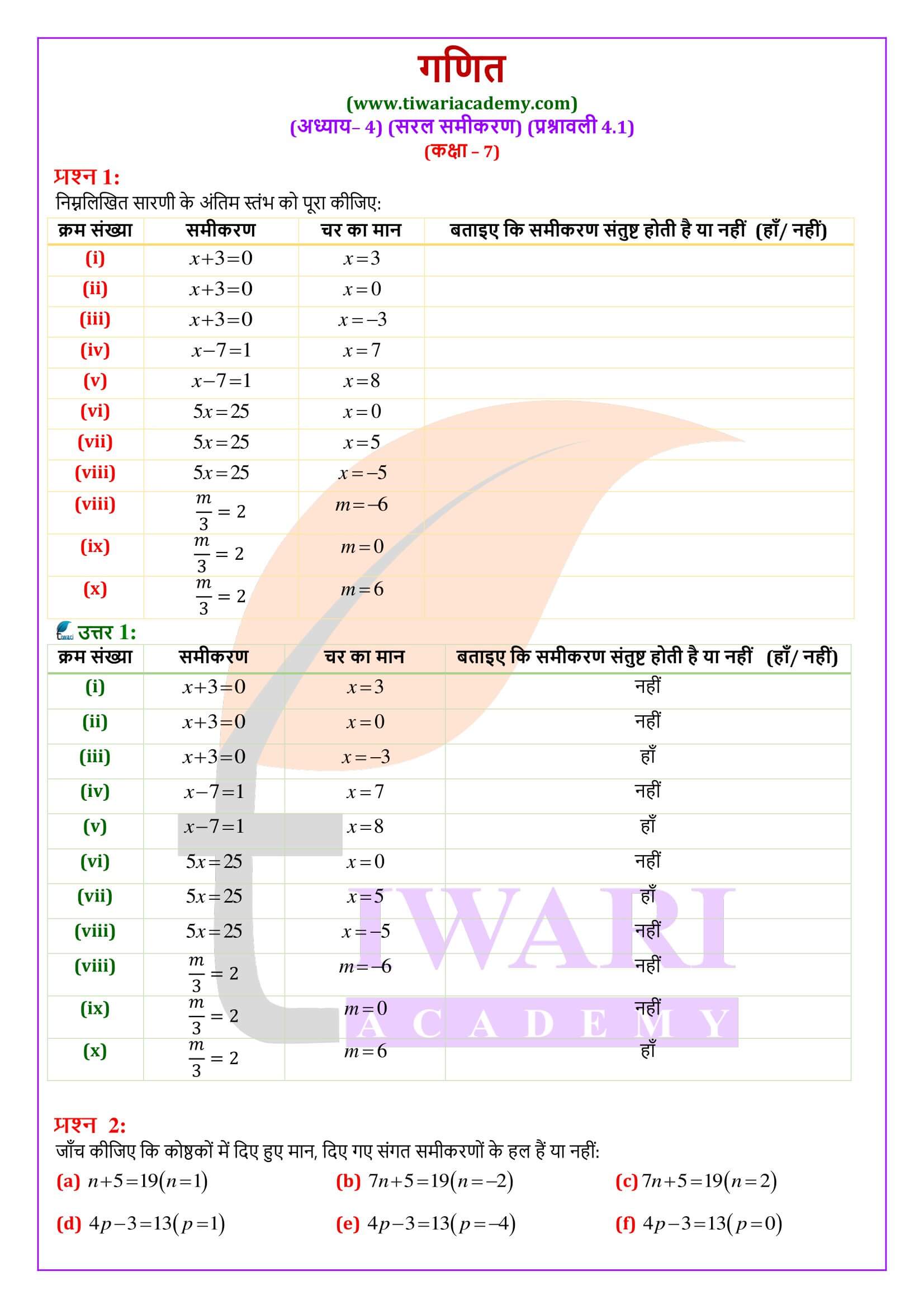
एनसीईआरटी समाधान कक्षा 7 गणित प्रश्नावली 4.1
सरल समीकरण
ऐसी समीकरण जिसमें केवल एक चर होता है तथा जिसकी घात भी एक होती है इस समीकरण को रैखिक समीकरण भी कहते हैं
उदाहरण:
ax + b = 0 जहाँ a ≠ 0
समीकरण बनाना
अमीना सारा से कोई संख्या सोचने को कहती है। अमीना संख्या के बारे में कुछ नहीं जानती है। उसके लिए, यह संख्या 1, 2, 3, …, 11, …, 100, … में से कुछ भी हो सकती है। आइए इस अज्ञात संख्या को एक अक्षर x से व्यक्त करें। आप ग के स्थान पर कोई अन्य अक्षर जैसे y, t इत्यादि का प्रयोग कर सकते हैं। सारा जब संख्या को 4 से गुणा करती है, तो उसे 4x प्राप्त होता है। फिर वह इस गुणनफल में 5 जोड़ती है और 4x + 5 प्राप्त करती है। (4x + 5) का मान x के मान पर निर्भर करता है। इस प्रकार, यदि x = 1 है, तो 4x + 5 = 4 ×1 + 5 = 9 है। इसका अर्थ है कि यदि सारा के मस्तिष्क में 1 होता, तो उसके द्वारा प्राप्त परिणाम 9 होता। इसी प्रकार, यदि उसने संख्या 5 सोची होती, तो उसका x = 5 के लिए 4x + 5 = 4 × 5 + 5 = 25, यानी, सारा ने यदि संख्या 5 सोची होती तो उसका परिणाम 25 होता।
समीकरण चर पर एक प्रतिबंध होता है। समीकरण में, चर x, y या कोई अन्य अक्षर भी हो सकता है।
चर
शब्द चर का अर्थ है, ऐसी कोई वस्तु जो विचरण कर, अर्थात् बदल सकती हो। एक चर विभिन्न संख्यात्मक मान ले (ग्रहण कर) सकता है, अर्थात् इसका मान निश्चित या स्थिर नहीं होता है। चरों को प्रायः अंग्रेजी वर्णमाला के अक्षरों x, y, z, l, m, n, p इत्यादि से व्यक्त किया जाता है। चरों से हम व्यंजकों को बनाते हैं। ये व्यंजक चरों पर योग, व्यवकलन, गुणन और विभाजन जैसी संक्रियाएँ करके प्राप्त किए (बनाए) जाते हैं।
समीकरण क्या है?
संक्षिप्त रूप में, एक समीकरण चर पर एक प्रतिबंध होता है। प्रतिबंध यह है कि दोनों व्यंजकों के मान बराबर होने चाहिए। ध्यान दीजिए कि इन दोनों व्यंजकों में से कम से कम एक में चर अवश्य होना चाहिए।
एक समीकरण में, समता या समिका का चिह्न सदैव होता है। समता का चिह्न यह दर्शाता है कि इस चिह्न के बाईं ओर के व्यंजक ¹बायाँ पक्ष का मान चिह्न के दाईं ओर के व्यंजक (दायाँ पक्ष) के मान के बराबर है।
समीकरण 4x + 5 = 65 है। समीकरण 10y – 20 = 50 है।
किसी समीकरण के बाएँ और दाएँ पक्षों के व्यंजकों को आपस में बदलने पर, समीकरण वही रहती है। यह गुण बहुधा समीकरणों को हल करने में उपयोगी रहता है।