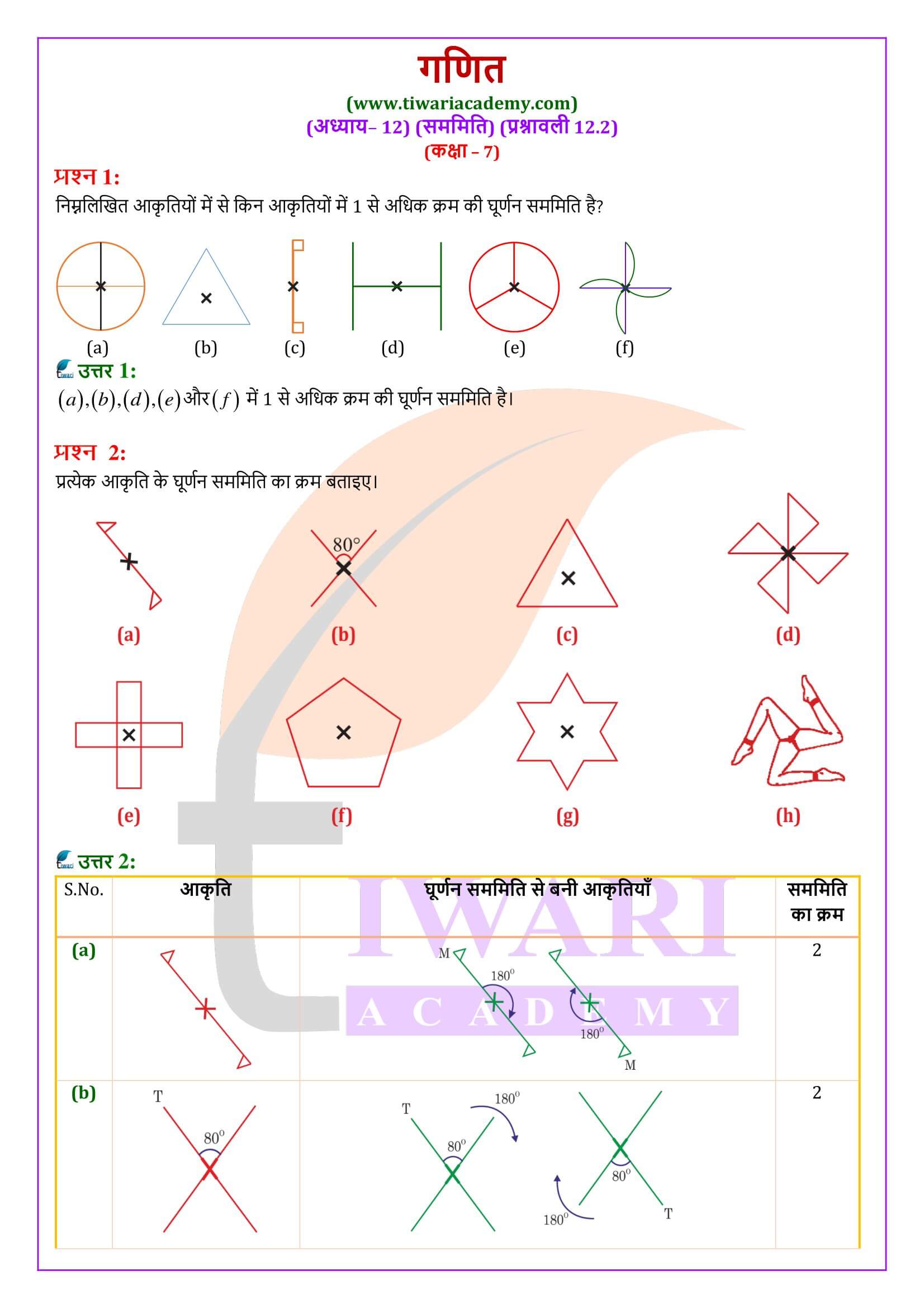
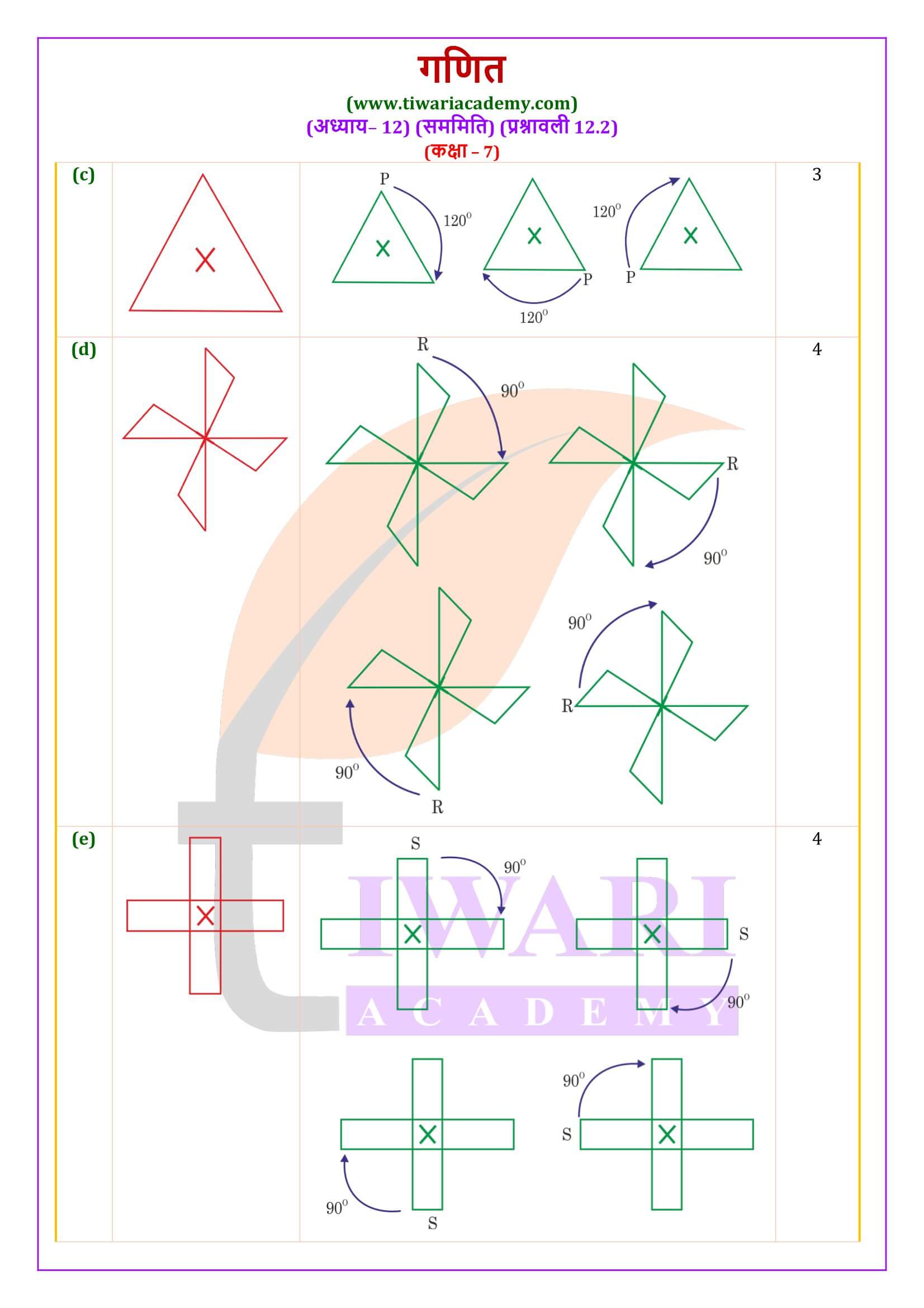
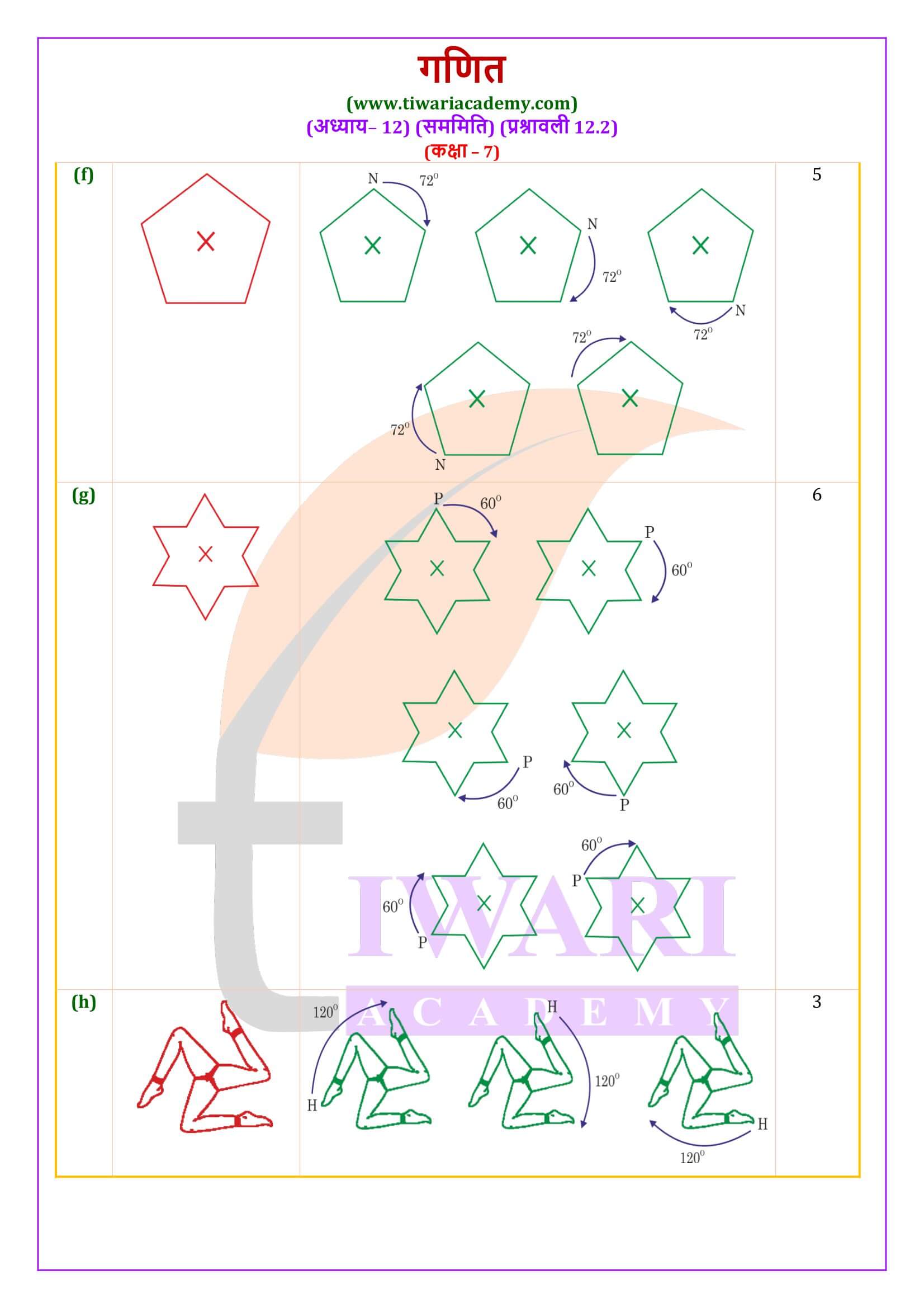
एनसीईआरटी समाधान कक्षा 7 गणित प्रश्नावली 12.2

घूर्णी समरूपता, जिसे ज्यामिति में रेडियल समरूपता के रूप में भी जाना जाता है, वह गुण है जो एक आकृति में होता है जब वह आंशिक मोड़ द्वारा कुछ घुमाव के बाद समान दिखता है। घूर्णी समरूपता की एक वस्तु की डिग्री अलग-अलग झुकावों की संख्या है जिसमें यह प्रत्येक रोटेशन के लिए बिल्कुल समान दिखता है।

उदाहरण:
यदि आप साइकिल के एक पहिए को घुमाते हैं, तो वह घूर्णन करता है। यह दोनों ही दिशाओं, अर्थात् दक्षिणावर्त और वामावर्त दिशाओं में घूर्णन कर सकता है।
(i) दक्षिणावर्त घूर्णन और
(ii) वामावर्त घूर्णन
घूर्णन के दौरान घूमे गए कोण को घूर्णन कोण कहते हैं। आप जानते हैं कि एक पूरे चक्कर में 360° का घूर्णन होता है।

1. एक आधे या अर्ध चक्कर
2. एक चौथाई चक्कर के घूर्णन कोणों के क्रमशः क्या माप हैं? एक अर्ध चक्र का अर्थ 180° का घूर्णन है तथा एक-चौथाई चक्कर का अर्थ 90° का घूर्णन है।

कागज की हवाई चकरी सममित दिखाई देती है, परंतु आपको इसकी कोई सममिति रेखा प्राप्त नहीं होती है। इसको किसी प्रकार से मोड़ने पर भी दोनों आधे भाग संपाती नहीं होंगे। यदि आप इसके केंद्र (बीच) वाले स्थिर (या निश्चत) बिदु के परित 90° के कोण पर घुमाएँ, तो आप देखेंगे की हवाई चकरी का आकार, पहले जैसा ही है। हम कहते हैं कि चकरी में एक घूर्णन सममिति है।
एक पूरे चक्कर में, ऐसी चार स्थितियाँ हैं (90°, 180°, 270° और 360° के कोणों पर घुमाने या घूर्णन करने पर), जब चकरी पहली जैसी ही दिखती है। इसी कारण, हम कहते हैं कि चकरी में क्रम 4 की घूर्णन सममिति है।

आइए इस वर्ग के केंद्र को × से अंकित करके इसके परित इस वर्ग को एक-चौथाई चक्कर पर घुमाएँ। केंद्र के चारों ओर 90° घूमाने पर वर्ग की आकृति में कोई बदलाव नहीं होता है। वर्ग को पुनः 90° के कोण पर घुमाइए (घूर्णन दीजिए)। इस प्रकार, जब आप वर्ग को चार एक-चौथाई चक्कर घुमा देते हैं, तो वह अपनी प्रारंभिक स्थिति पर आ जाती है।

इस प्रकार, एक वर्ग में उसके केंद्र के चारों ओर क्रम 4 की घूर्णन सममिति होती है। ध्यान दीजिए कि इस स्थिति में,

• (i) घूर्णन का केंद्र वर्ग का केंद्र है।
• (ii) घूर्णन का कोण 90° है।
• (iii) घूर्णन की दिशा दक्षिणावर्त है।
• (iv) घूर्णन सममिति का क्रम 4 है।