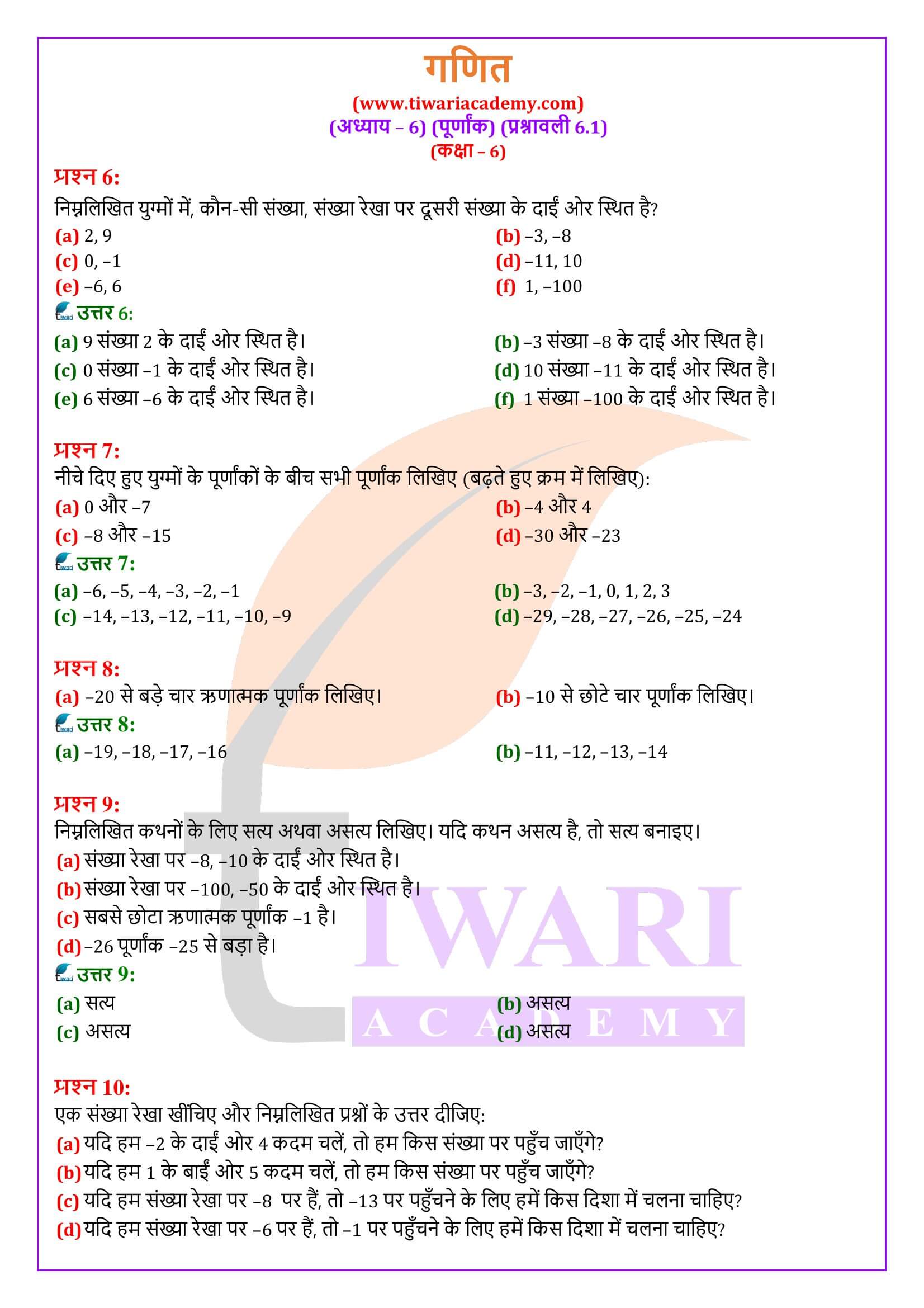
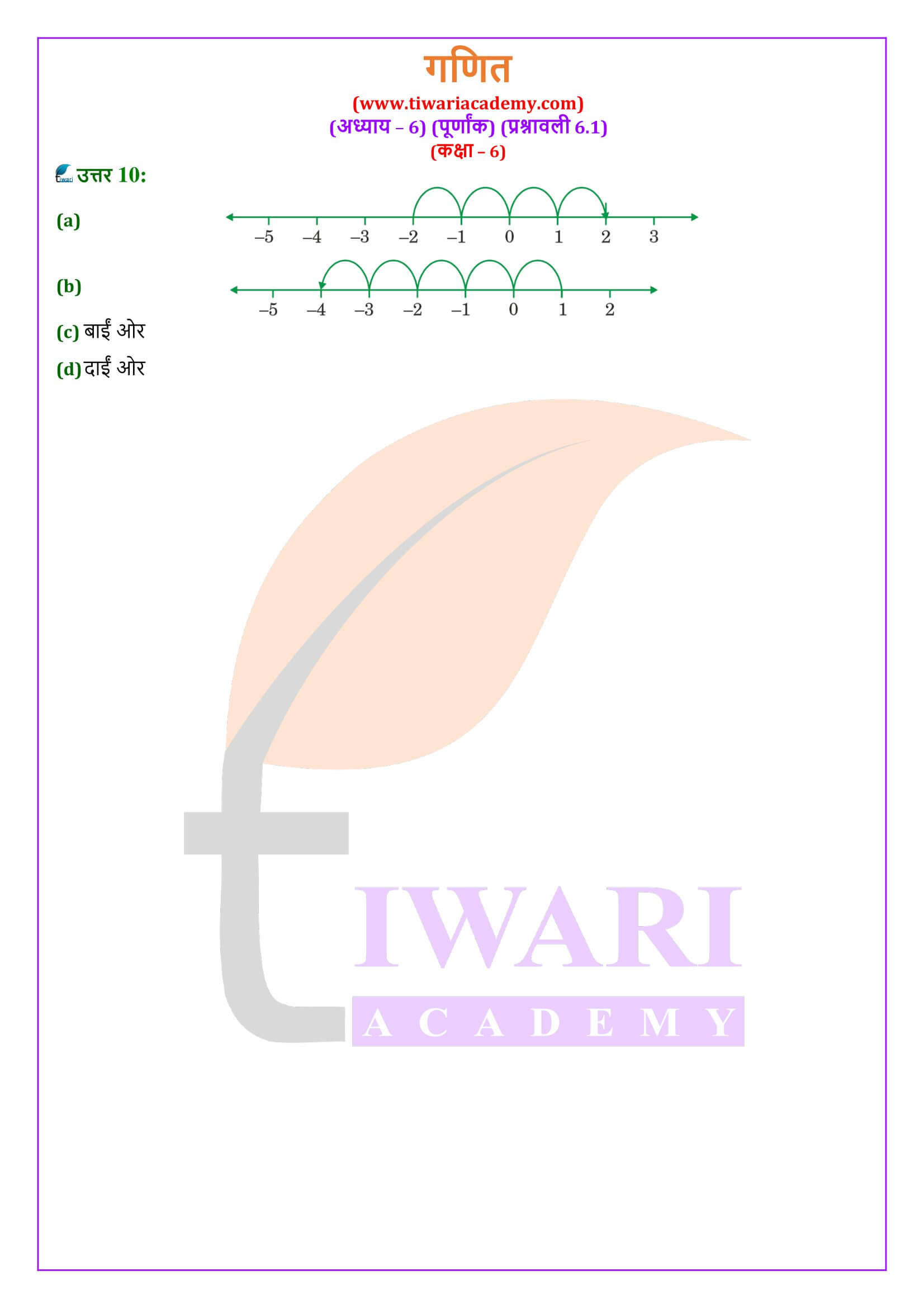
एनसीईआरटी समाधान कक्षा 6 गणित प्रश्नावली 6.1

गणित में शून्य से अधिक मान रखने वाली संख्याएँ धनात्मक संख्या कहलाती है। वह संख्या जो किसी भी संख्या रेखा में शून्य के दायें ओर स्थित सभी संख्याएँ धनात्मक संख्या कहलाती है। ये प्राकृतिक संख्याएँ होती हैं तथा इनका मान सदैव 0 से अधिक होता है।
ऋणात्मक संख्याए
गणित में, ऋणात्मक संख्या एक वास्तविक संख्या होती है जो शून्य से कम होती है। वह संख्या जो किसी भी संख्या रेखा में शून्य के बायें ओर स्थित सभी संख्याएँ ऋणात्मक संख्या कहलाती है।
कौन कहाँ है
मान लीजिए डेविड और मोहन ने 0 स्थान से विपरीत दिशाओं में चलना प्रारंभ कर दिया है। मान लीजिए कि 0 के दाईं ओर चले कदमों को + चिह्न से निरूपित किया जाता है और 0 से बाईं ओर चले कदमों को – चिह्न से निरूपित किया जाता है। यदि मोहन शून्य के दाईं ओर 5 कदम चलता है, तो उसे + 5 से निरूपित किया जा सकता है और यदि डेविड शून्य के बाईं ओर 5 कदम चलता है, तो उसे – 5 से निरूपित किया जा सकता है।

दी गई प्राकृत संख्या में यदि 1 जोड़ दे तो अगली प्राकृत संख्या प्राप्त होती है। प्राप्त संख्या को दी गयी संख्या की परवर्ती संख्या कहते है।
निम्नलिखित संख्याओं के परवर्ती लिखिए:
संख्या – परवर्ती
10 – 11
8 – 9
– 5, – 4
– 3, – 2
0 – 1

पूर्ववर्ती संख्या
दी गई प्राकृत संख्या में यदि 1 घटा दे तो पिछली प्राकृत संख्या प्राप्त होती है। प्राप्त संख्या को दी गयी संख्या की पूर्ववर्ती संख्या कहते है।
अब निम्नलिखित संख्याओं के पूर्ववर्ती लिखिए:
संख्या – पूर्ववर्ती
10 – 9
8 – 7
5 – 4
3 – 2
0 – 1

सबसे पहले ज्ञात की गईं संख्याएँ प्राकृत संख्याएँ, अर्थात् 1, 2, 3, 4, … हैं। यदि हम प्राकृत संख्याओं के संग्रह में शून्य को सम्मिलित कर लेते हैं, तो हमें संख्याओं का एक नया संग्रह प्राप्त होता है। इन संख्याओं को पूर्ण संख्याएँ कहते हैं। इस प्रकार 0, 1, 2, 3, 4, … पूर्ण संख्याएँ हैं। अब हमें ज्ञात हो गया है कि ऋणात्मक संख्याएँ, जैसे -1, -2, -3, -4, … भी होती हैं। यदि हम पूर्ण संख्याओं और इन ऋणात्मक संख्याओं को मिला लें, तो हमें संख्याओं का एक नया संग्रह प्राप्त होगा, जो, 1, 2, 3, 4, …, -1, -2, -3, -4, … है। संख्याओं के इस संग्रह को पूर्णांकों का संग्रह कहते हैं। इस संग्रह में 1, 2, 3, 4, … धनात्मक पूर्णांक कहलाते हैं और -1, -2, -3, -4, … ऋणात्मक पूर्णांक कहलाते हैं।

• (a) प्रत्येक धनात्मक पूर्णांक प्रत्येक ऋणात्मक पूर्णांक से बड़ा होता है।
• (b) शून्य प्रत्येक धनात्मक पूर्णांक से छोटा होता है।
• (c) शून्य प्रत्येक ऋणात्मक पूर्णांक से बड़ा होता है।
• (d) शून्य न तो एक ऋणात्मक पूर्णांक है और न ही एक धनात्मक पूर्णांक है।
• (e) कोई संख्या शून्य से दाईं ओर जितनी अधिक दूरी पर होगी उतनी ही बड़ी होगी।
• (f) कोई संख्या शून्य से बाईं ओर जितनी अधिक दूरी पर होगी, उतनी ही छोटी होगी।