एनसीईआरटी समाधान कक्षा 7 गणित प्रश्नावली 12.3
एनसीईआरटी समाधान कक्षा 7 गणित प्रश्नावली 12.3 सममिति के हल अभ्यास के सवाल जवाब हिंदी और अंग्रेजी में सीबीएसई तथा राजकीय बोर्ड सत्र 2025-26 के लिए यहाँ दिए गए हैं। कक्षा 7 गणित के छात्र अध्याय 12.3 में घूर्णन सममिति के बारे में चित्रों के माध्यम से पढ़ते हैं। प्रत्येक प्रश्न को चित्रों के माध्यम से हल करके समझाया गया है।
एनसीईआरटी समाधान कक्षा 7 गणित प्रश्नावली 12.3
रैखिक सममिति और घूर्णन सममिति
कुछ आकारों में केवल रैखिक सममिति होती है, कुछ में केवल घूर्णन सममिति होती है तथा कुछ आकारों में रैखिक तथा घूर्णन दोनों प्रकार की सममितियाँ होती हैं।
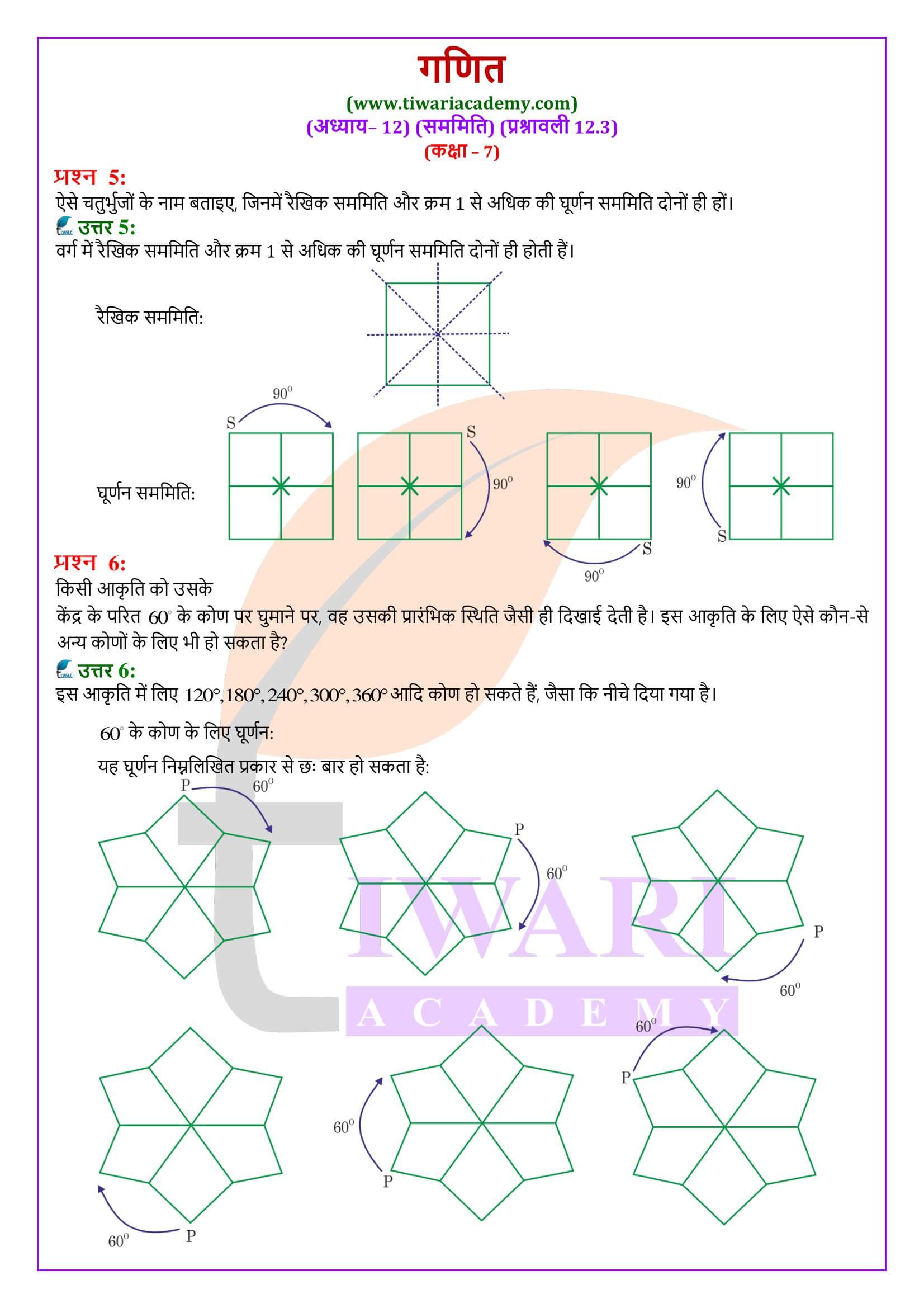
अभ्यास 12.3 के लिए उदाहरण
एक वृत्त सबसे अधिक पूर्ण सममित आकृति है, क्योंकि इसको इसके केंद्र के परित किसी भी कोण पर घुमा कर वही आकृति प्राप्त की जा सकती है, अर्थात् इसमें अपरिमित रूप से अनेक क्रम की घूर्णन सममिति है तथा साथ ही इसकी अपरिमित सममित रेखाएँ हैं। वृत्त के किसी भी प्रतिरूप को देखिए। केंद्र से होकर जाने वाली प्रत्येक रेखा (अर्थात् प्रत्येक व्यास) परावर्तन सममिति की एक सममिति रेखा है तथा केंद्र के परित प्रत्येक कोण के लिए इसकी एक घूर्णन सममिति है।
घूर्णन सममिति का क्रम
प्रत्येक वस्तु (या आकृति) में, क्रम 1 की घूर्णन सममिति होती है, क्योंकि आकृति के घूर्णन के बाद (अर्थात् पूरे एक चक्कर के बाद) वह अपनी प्रारंभिक स्थिति में आ जाता है।
अंग्रेजी वर्णमाला के कुछ अक्षरों में सममिति
अंग्रेजी वर्णमाला के कुछ अक्षरों में अद्भुत एवं आकर्षक सममितीय संरचनाएँ हैं। किन बड़े अक्षरों में केवल एक ही सममित रेखा है (जैसे E)? किन बड़े अक्षरों में क्रम 2 की घूर्णन सममिति है (जैसे I)?
वर्णमाला का अक्षर – रैखिक सममित – घूर्णन सममित
Z – नहीं – हाँ
H – हाँ – हाँ
O – हाँ – हाँ
E – हाँ – –
N – – – हाँ
कक्षा 7 गणित अध्याय 12.3 के लिए महत्वपूर्ण तथ्य
- 1. एक आकृति मे रैखिक सममिति तब होती है, जब कोई ऐसी रेखा प्राप्त की जा सके जिसके अनुदिश उस आकृति को मोड़ने पर, उसके दोनों भाग परस्पर संपाती हो जाएँ।
- 2. सम बहुभुजों में बराबर भुजाएँ और बराबर कोण होते हैं। उनकी अनेक अर्थात् एक से अधिक, सममित रेखाएँ होती हैं।
- 3. प्रत्येक सम बहुभुज की उतनी ही सममित रेखाएँ होती हैं, जितनी उसकी भुजाएँ होती हैं।
- 4. दर्पण परावर्तन से ऐसी सममिति प्राप्त होती है, जिसमें बाएँ-दाएँ अभिमुखों का ध्यान रखना होता है।
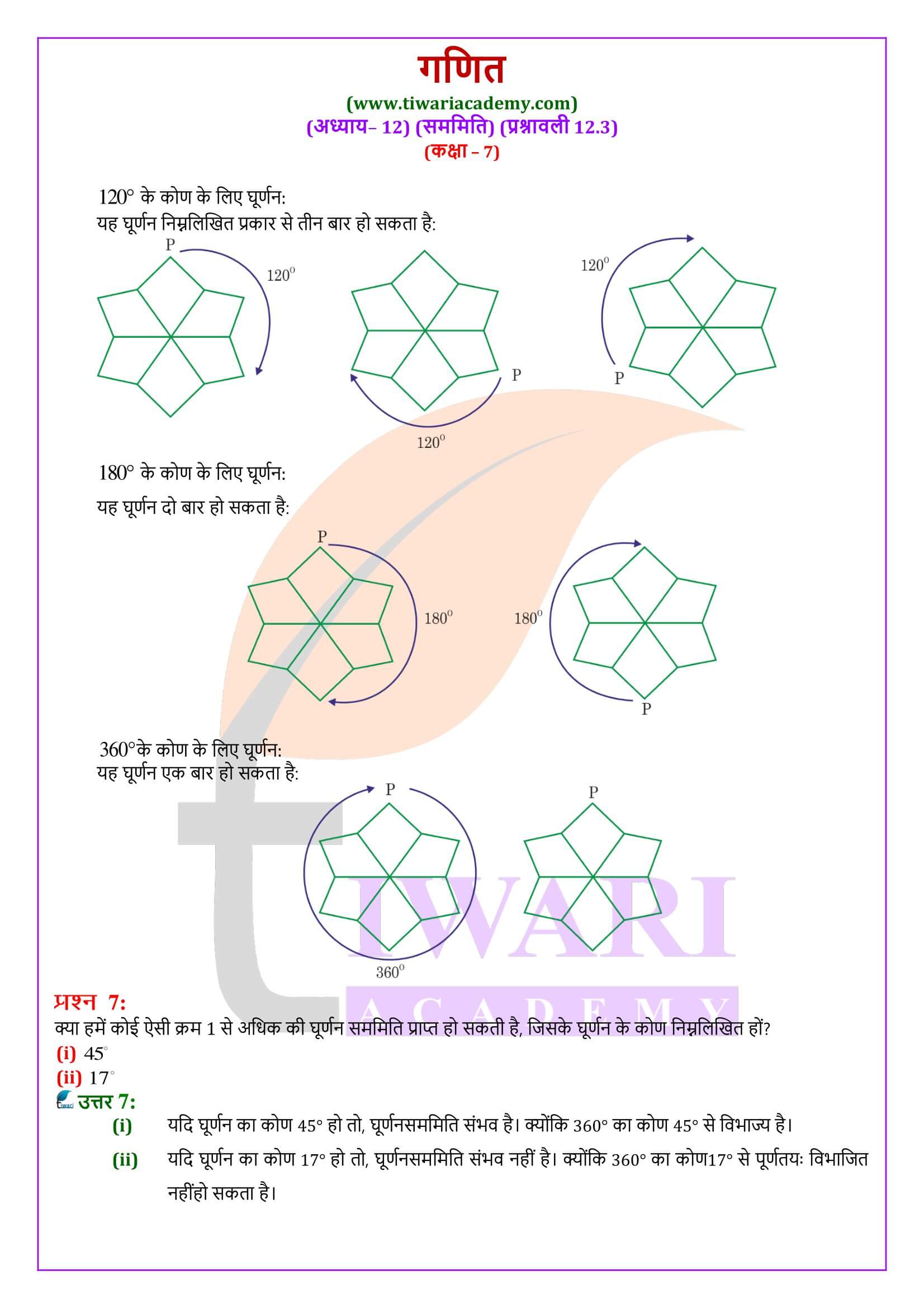
- 5. घूर्णन में एक वस्तु को एक निश्चित बिदु के परित घुमाया जाता है। यह निश्चित बिदु घूर्णन का केंद्र कहलाता है। जिस कोण पर वस्तु घूमती है, उसे घूर्णन का कोण कहते हैं। आधे या अर्ध चक्कर का अर्थ 180° का घूर्णन है तथा एक-चौथाई चक्कर का अर्थ 90° का घूर्णन है। घूर्णन दक्षिणावर्त और वामावर्त दोनों ही दिशाओं में हो सकता है।
- 6. यदि घूर्णन के बाद, वस्तु, स्थिति के अनुसार, पहले जैसी ही दिखाई देती है, तो हम कहते हैं कि उसमें घूर्णन सममिति है।
- एक पूरे चक्कर (360° के) में, एक वस्तु जितनी बार स्थिति के अनुसार, पहले जैसी ही दिखाई देती है, वह संख्या उस घूर्णन सममिति का क्रम कहलाती है। उदाहरणार्थ, एक वर्ग की घूर्णन सममिति का क्रम 4 है तथा एक समबाहु त्रिभुज की घूर्णन सममिति का क्रम 3 है।
- कुछ आकारों में केवल एक ही सममिति रेखा होती है, जैसे अक्षर E कुछ में केवल घूर्णन सममिति ही होती है, जैसे अक्षर S तथा कुछ में दोनों प्रकार की सममितियाँ होती हैं, जैसे अक्षर H है। सममिति का अध्ययन इसलिए महत्वपूर्ण है, क्योंकि इसका दैनिक जीवन में अधिकांशतः प्रयोग होता है तथा इससे भी अधिक महत्व इस कारण है कि यह हमें सुंदर एवं आकर्षक डिज़ाइन प्रदान कर सकती है।