एनसीईआरटी समाधान कक्षा 9 गणित प्रश्नावली 12.1
एनसीईआरटी समाधान कक्षा 9 गणित प्रश्नावली 12.1 सांख्यिकी के हल सीबीएसई सत्र 2025-26 के लिए हिंदी और अंग्रेजी मीडियम में यहाँ से प्राप्त किए जा सकते हैं। कक्षा 9 गणित की प्रश्नावली 12.1 के सभी प्रश्नों को चरण-दर-चरण सरल भाषा में हल करके यहाँ दी गई पीडीएफ में दिखाया गया है। जिन विद्यार्थियों को पीडीएफ समाधान के माध्यम से समझ न आए वे विडियो समाधान की मदद लेकर प्रश्नों के हल आसानी से समझ सकते हैं।
एनसीईआरटी समाधान कक्षा 9 गणित प्रश्नावली 12.1
कक्षा 9 गणित अध्याय 12 प्रश्नावली 12.1 के लिए एनसीईआरटी समाधान
आंकड़ों का आलेखीय निरुपण
एकत्रित किये गए आंकड़ों को चित्रात्मक (ग्राफ़) रूप से प्रस्तुत करने को आंकड़ों का आलेखीय निरुपण कहलाता है।
प्रायः अलग-अलग मदों की तुलनाओं को आलेखों की सहायता से अच्छी तरह से दर्शाया जाता है। तब वास्तविक आंकड़ों की तुलना में इस निरूपण को समझना अधिक सरल हो जाता है। इस अनुच्छेद में, हम निम्नलिखित आलेखीय निरूपणों का अध्ययन करेंगे।
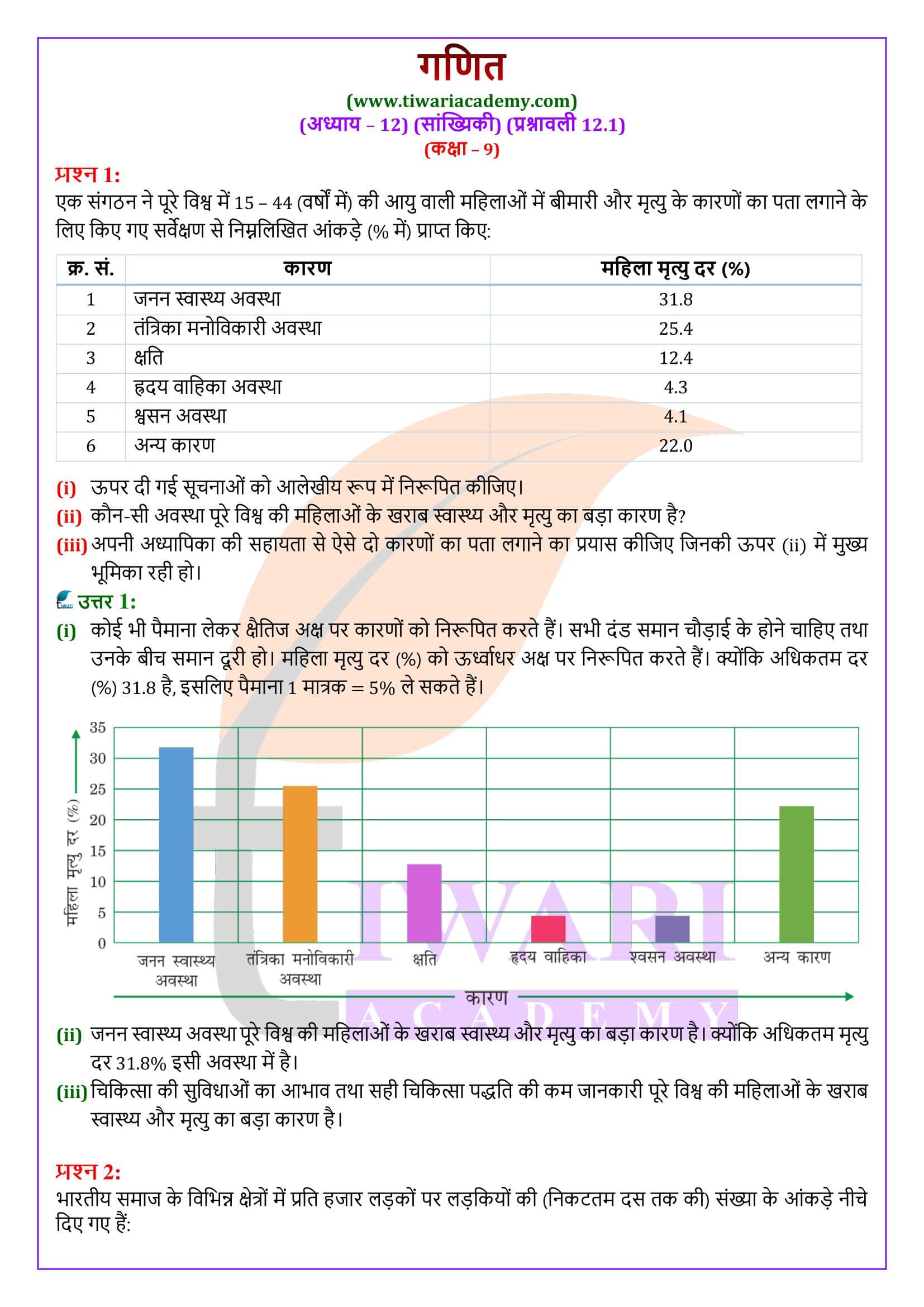
- (i) दंड आलेख
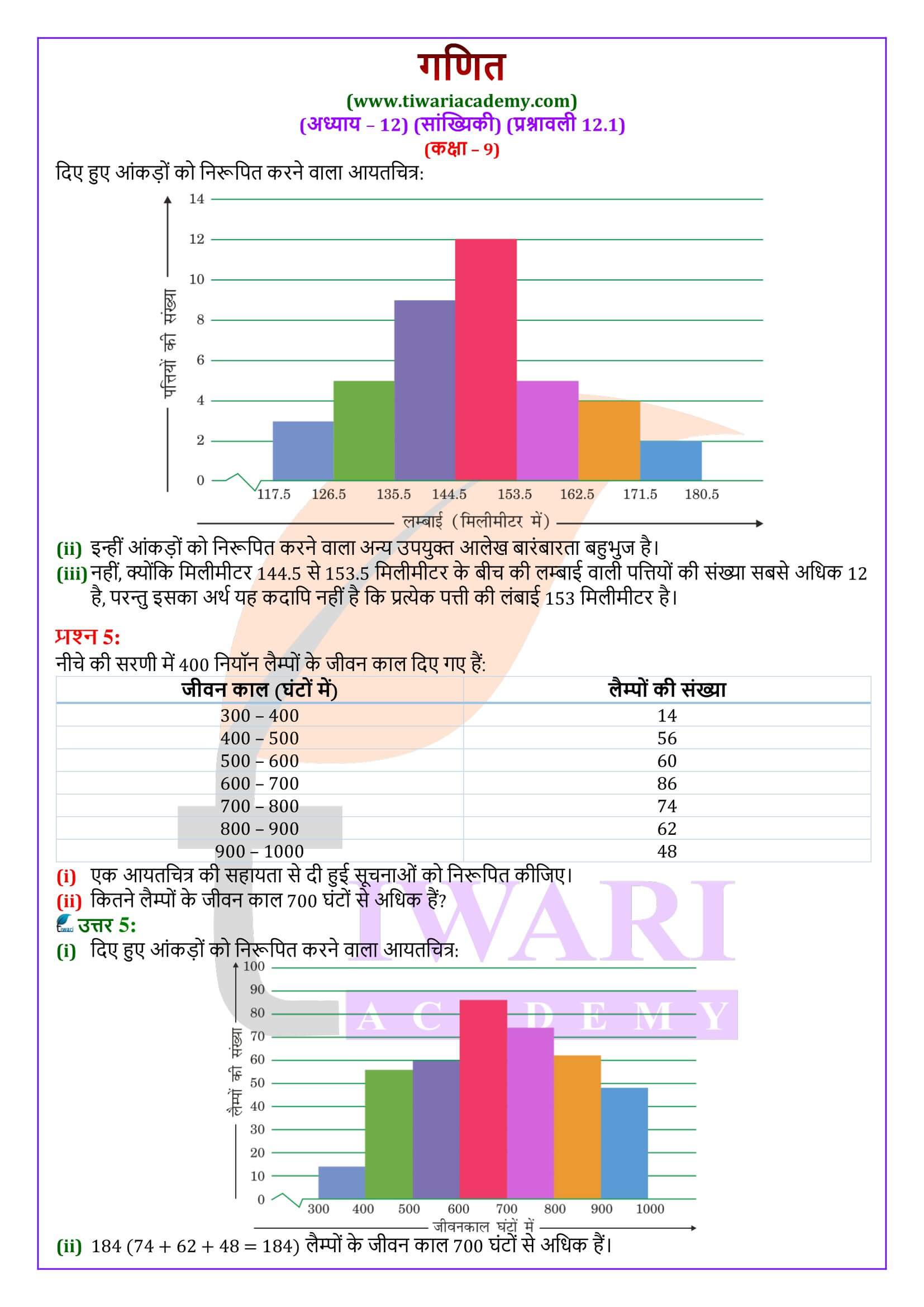
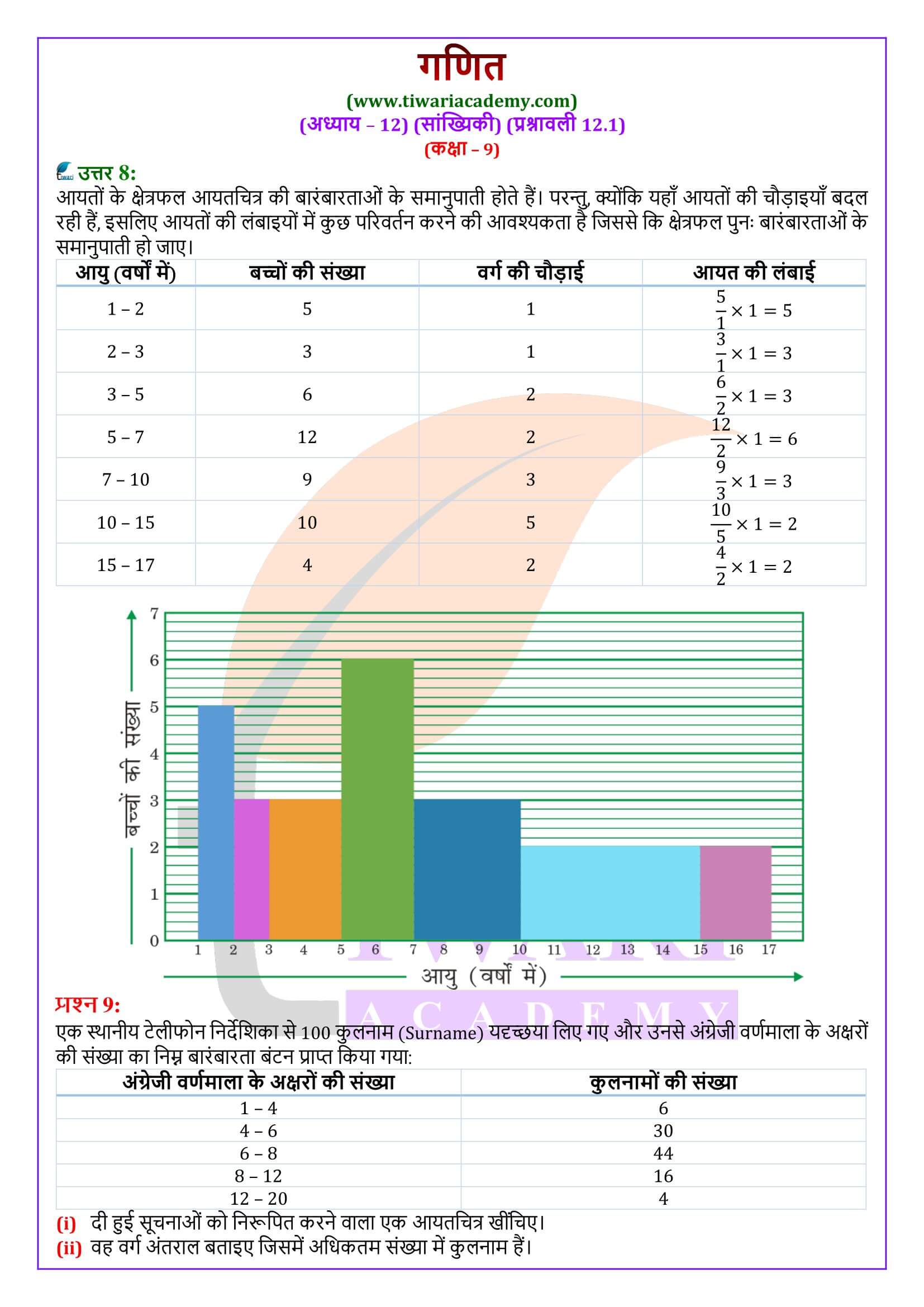
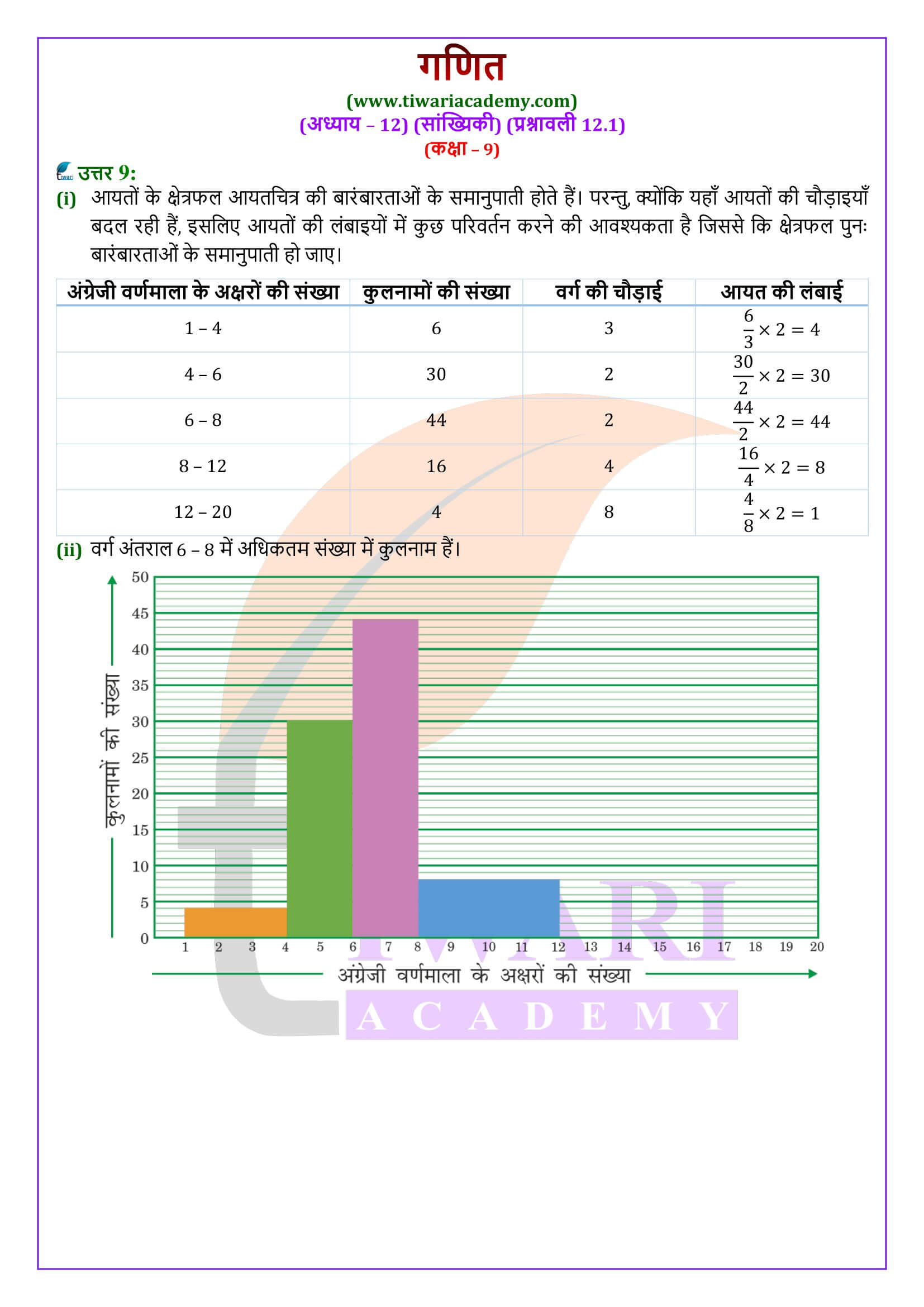
- (ii) एकसमान चौड़ाई और परिवर्ती चौड़ाइयों वाले आयतचित्र
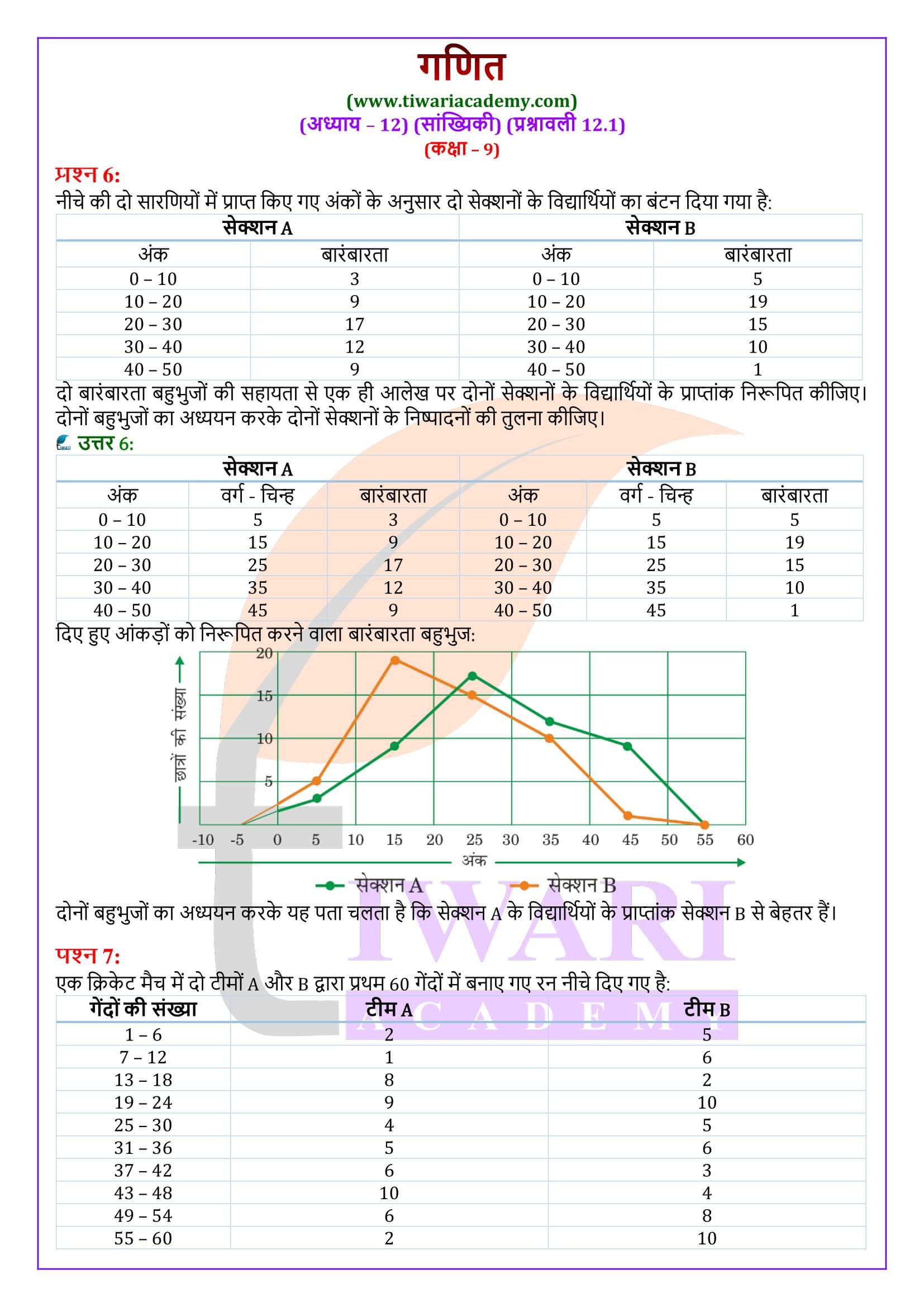
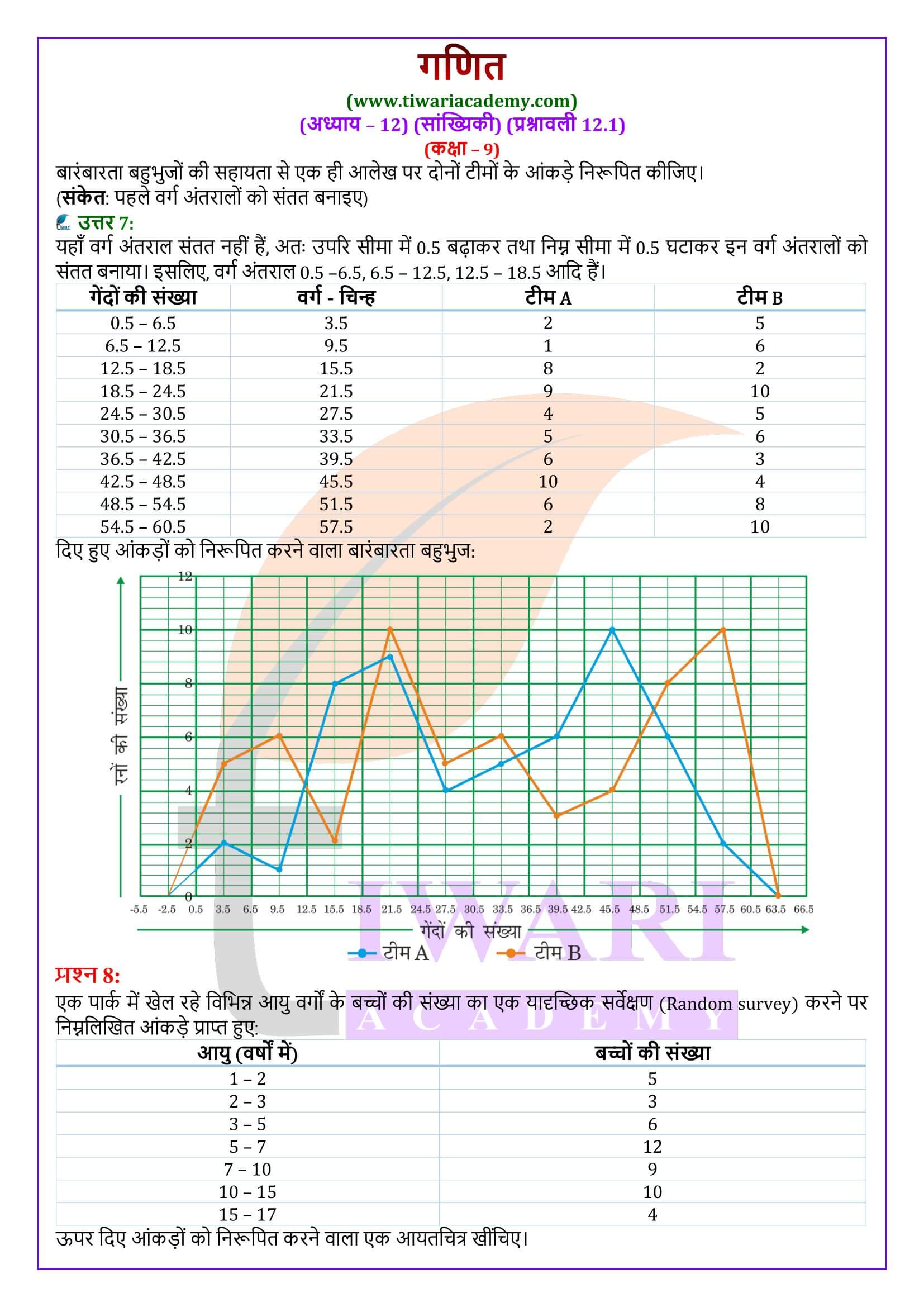
- (iii) बारंबारता बहुभुज
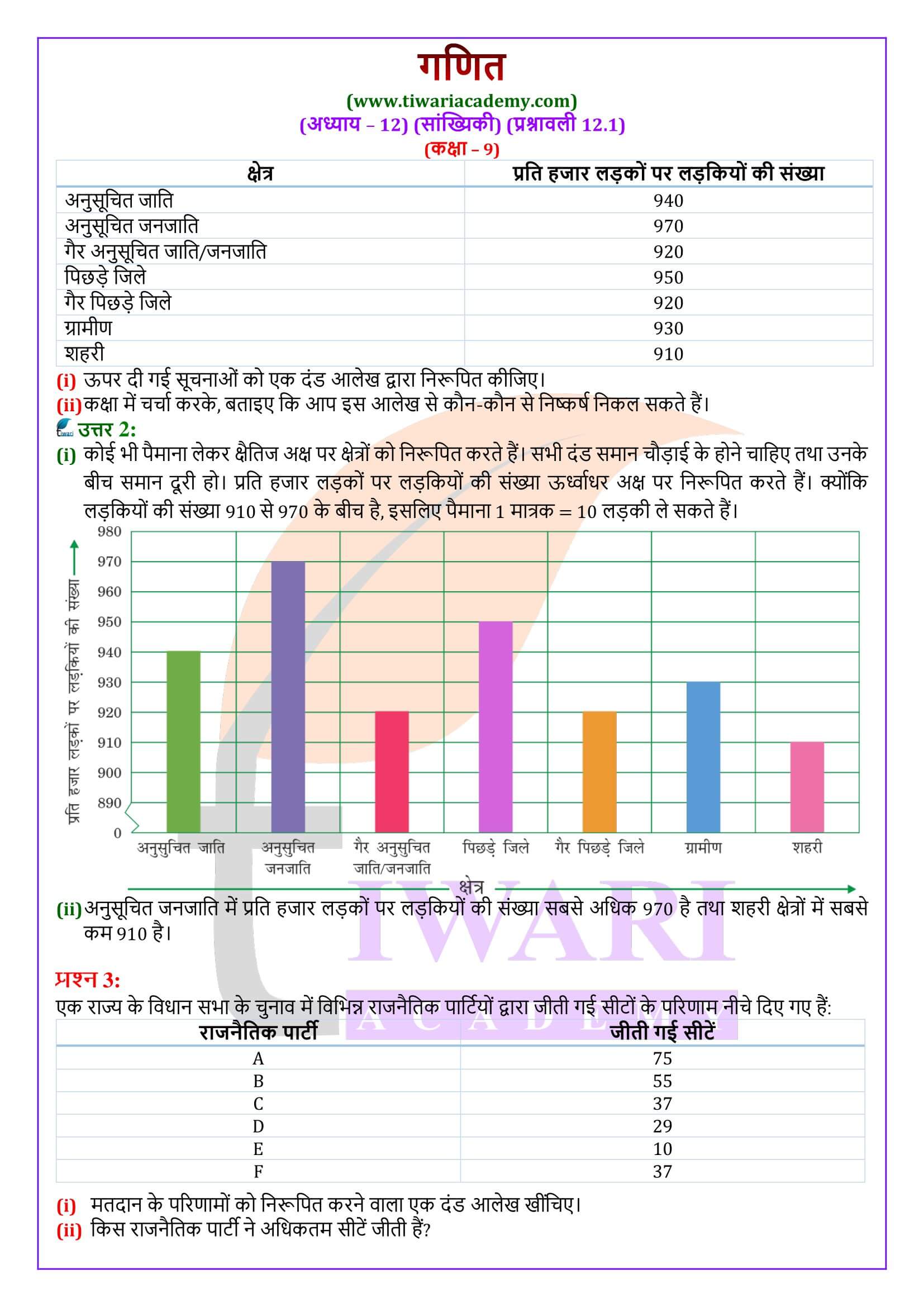
दंड आलेख
यह आंकड़ों का एक चित्रीय निरूपण होता है जिसमे प्रायः एक अक्ष (मान लीजिए x अक्ष ) पर एक चर को प्रकट करने वाले एक समान चौड़ाई के दंड खींचे जाते है। दूसरे चर के मान दूसरे अक्ष (मान लीजिए y अक्ष) पर दिखाए जाते हैं। दण्डों की ऊंचाई चर के मान पर निर्भर करती है।
बारंबारता बहुभुज
बारंबारता बहुभुज वह नाम है जो एक चार्ट क्लास प्राप्त करता है जो एक आवृत्ति हिस्टोग्राम से बनाया जाता है। ये हिस्टोग्राम्स आवृत्तियों को प्रतिबिंबित करने के लिए ऊर्ध्वाधर स्तंभों का उपयोग करते हैं। आवृत्ति बहुभुज इन स्तंभों के उच्चतम बिंदुओं को जोड़कर बनाया जाता है।
संचयी आवृत्ति वक्र
संचयी आवृत्ति चित्रों में हम समस्त समान आवृत्तियों को किसी विशेष क्रम (घटते या बढ़ते) से संचित करते जाते हैं और फिर संचित आवृत्तियों के आधार पर ऊँची या नीची सीमाएँ प्रदर्शित करने के लिए वक्र खींचते हैं। इन चित्रों को तोरण या ओगाइव भी कहते हैं।
वर्ग-चिह्न
वर्ग अंतरालों के इन मध्य-बिंदुओं को वर्ग-चिह्न कहा जाता है। किसी वर्ग अंतराल का वर्ग-चिह्न ज्ञात करने के लिए, हम उस वर्ग अंतराल की उपरि सीमा और निम्न सीमा का योग ज्ञात करते हैं और इस योग को 2 से भाग दे देते हैं।
इस तरह,
वर्ग-चिह्न = (उपरि सीमा + निम्न सीमा)/2
बारंबारता बहुभुज का प्रयोग
बारंबारता बहुभुज का प्रयोग तब किया जाता है जबकि आंकड़ें संतत और बहुत अधिक होते हैं। यह समान प्रकृति के दो अलग-अलग आंकड़ों की तुलना करने में, अर्थात् एक ही कक्षा के दो अलग-अलग सेक्शनों के प्रदर्शनों की तुलना करने में अधिक उपयोगी होता है।