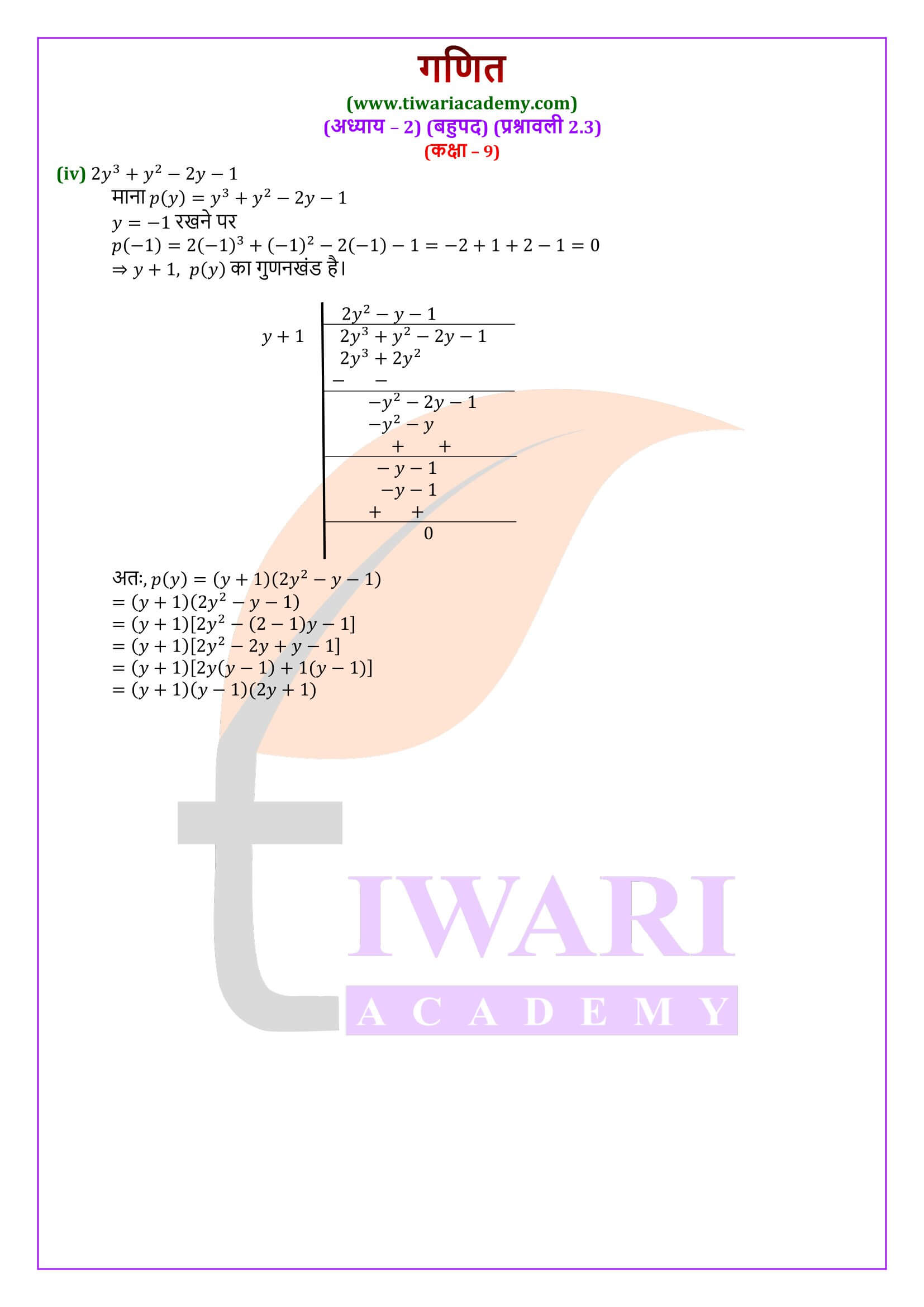
एनसीईआरटी समाधान कक्षा 9 गणित प्रश्नावली 2.3

बहुपद के शून्यक किसी बहुपद मे चर के स्थान पर किसी वास्तविक संख्या को प्रतिस्थापित करने पर यदि बहुपद का मान शून्य आ जाये तो वह वास्तविक संख्या बहुपद का शून्यक कहलाती है।
उदाहरण: ax – b का शून्ययक b/a है।

उदाहरण के लिए एक रैखिक बहुपद p(x) = ax + b जहाँ a ≠ 0 हो, तो p(x) का शून्यक एक होता हैं। जिसका मान –b/a है।
= – (अचर पद) / (x का गुणांक)
यहाँ अचर पद b है तथा x का गुणांक a है।

मान लीजिए कि p(x) एक से अधिक या उसके बराबर घात का कोई बहुपद है और मान लीजिए कि a कोई वास्तविक संख्या है। यदि p(x) को रैखिक बहुपद x – a से विभाजित किया जाता है, तो शेषफल p(a) होता है।
उदाहरण:
बहुपद p(x) = 2x ⁴ – 3x³ + 3x + 1 को x + 1 से भाग देने पर शेषफल ज्ञात कीजिए।
हल:
p(x) = 2x⁴ – 3x³ + 3x + 1) में x = -1 रखने पर
p(-1) = 2 (-1)⁴ – 3(-1)³ + 3(-1) + 1
p(-1) = 2 × 1 -3 × -1 + 3 × -1 + 1
= 3
शेषफल = 3

यदि बहुपद p(x) को बहुपद g(x) से विभाजित किया जाए और शेषफल r(x) = 0 हो तो बहुपद g(x) बहुपद p(x) का एक गुणनखंड होगा या हम कह सकते हैं कि यदि g(x), p(x) का एक गुणनखंड है, तो शेषफल r(x) शून्य होगा।

माना p(x) = x² + 4x + 3 और x + 1, p(x) का एक गुणनखंड है।
इसप्रकार, x = -1 के लिए p(x) का मान 0 होगा
इसके सत्यापन्न के लिए x = -1, p(x) में रखते हैं
p(-1) = (-1)² + 4 (-1) + 3
= 1 – 4 + 3
p(-1) = 0
जिससे सिद्ध होता है कि x + 1, p(x) का एक गुणनखंड है।