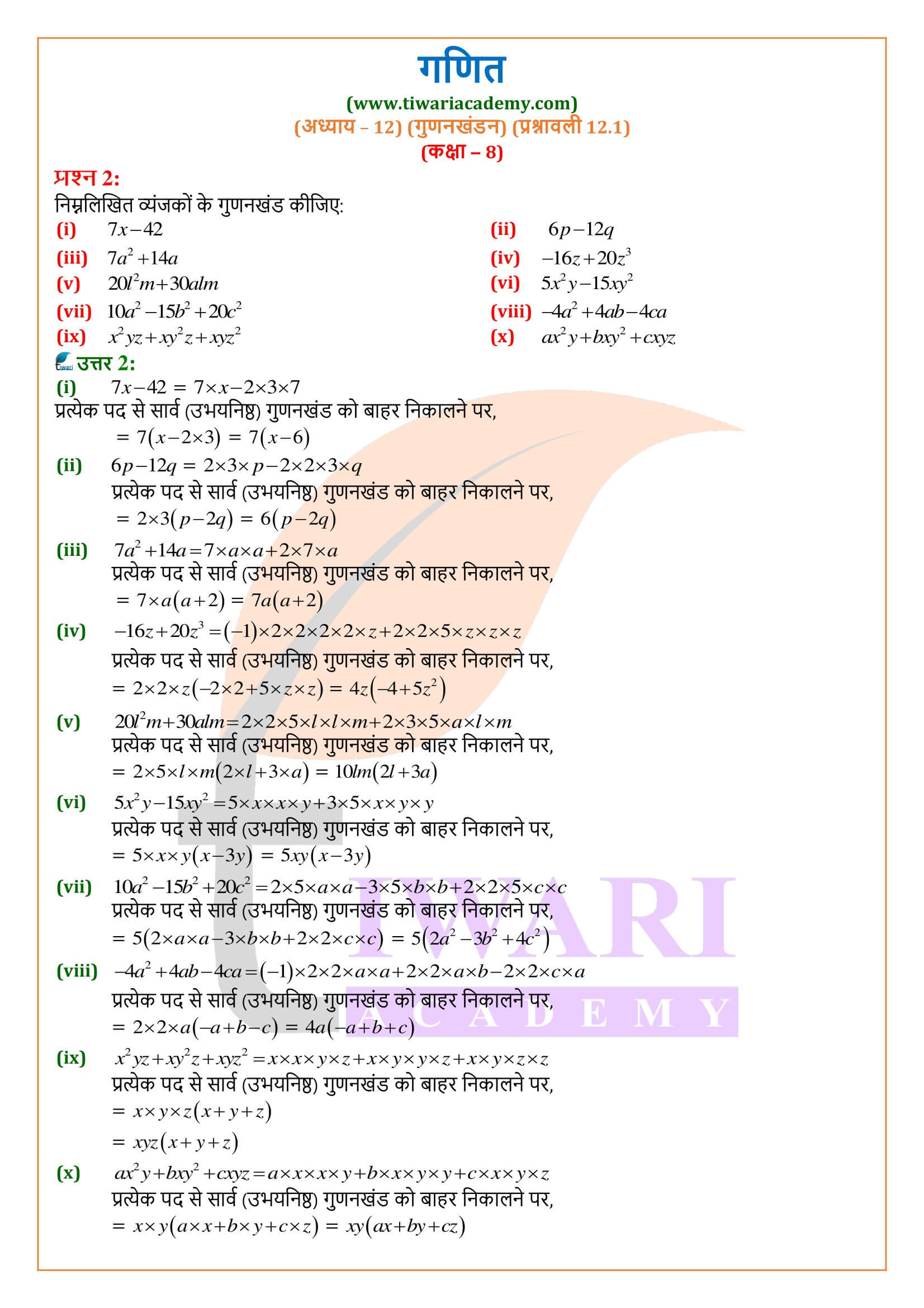
एनसीईआरटी समाधान कक्षा 8 गणित प्रश्नावली 12.1

एक प्राकृत संख्या लेते हैं। मान लीजिए यह संख्या 30 है। हम इसे अन्य प्राकृत संख्याओं के गुणनफल के रूप में लिखते हैं। जैसे:
30 = 2 × 15
= 3 × 10 = 5 × 6
इस प्रकार 1, 2, 3, 5, 6, 10, 15 और 30 संख्या 30 के गुणनखंड हैं। इनमें से 2, 3 और 5, संख्या 30 के अभाज्य गुणनखंड हैं। जब कोई संख्या अभाज्य गुणनखंडों के गुणनफल के रूप में लिखी हो, तो वह उसका अभाज्य गुणनखंड रूप कहलाता है। उदाहरण के लिए 30 को अभाज्य गुणनखंड रूप में 2 × 3 × 5 लिखते हैं।
70 का अभाज्य गुणनखंड रूप 2 × 5 × 7 है। 90 का अभाज्य गुणनखंड रूप 2 × 3 × 3 × 5 है, इत्यादि।

बीजीय व्यंजकों के पद गुणनखंडों के गुणनफलों के रूप में बनते हैं।
उदाहरणार्थ, बीजीय व्यंजक 5xy + 3x में, पद 5xy गुणनखंडों 5, x और y से बना है , अर्थात् 5xy = 5× x × y
ध्यान दीजिए कि 5xy के गुणनखंड 5, x और y को और आगे गुणनखंडित नहीं किया जा सकता है, अर्थात् उन्हें गुणनखंडों के गुणनफल के रूप में व्यक्त नहीं किया जा सकता है। हम कह सकते हैं कि 5गल के अभाज्य गुणनखंड 5, x और y हैं। बीजीय व्यंजकों में, हम ‘अभाज्य’ के स्थान पर शब्द ‘अखंडनीय का प्रयोग करते हैं। हम कहते हैं कि 5xy का अखंडनीय रूप 5 × x × y है।
अब, व्यंजक 3x (x + 2) पर विचार कीजिए। इसे गुणनखंडों 3, x और (x + 2) के गुणनफल के रूप में व्यक्त किया जा सकता है। अर्थात
3x (x + 2) = 3× x × (x + 2)
व्यंजक 3x (x + 2) के अखंडनीय गुणनखंड 3, x और (x + 2) हैं।

हम एक सरल उदाहरण से प्रारंभ करते हैं: 2x, 4 के गुणनखंड कीजिए। हम इसके प्रत्येक पद को अखंडनीय गुणनखंडों के गुणनफल के रूप में लिखेंगे:
2x = 2 × x
4 = 2 × 2
अतः 2x + 4 = (2 × x) + (2 × 2)
ध्यान दीजिए कि गुणनखंड 2 दोनों पदों में उभयनिष्ठ (सार्व) है।
देखिए, बंटन नियम द्वारा
2 × (x + 2) = (2 × x) + (2 × 2)
अतः हम लिख सकते हैं कि
2x + 4 = 2 × (x + 2) = 2 (x + 2)
इस प्रकार, व्यंजक 2x + 4 वही है जो 2 (x + 2) है। अब हम इसके गुणनखंड पढ़ सकते हैं:
ये 2 और (x + 2) हैं। ये गुणनखंड अखंडनीय हैं।

व्यंजक 2xy + 2y + 3x + 3 पर विचार कीजिए। आप देखेंगे कि पहले दो पदों में सार्व गुणनखंड 2 और y हैं तथा अंतिम दो पदों में सार्व गुणनखंड 3 है। परंतु सभी पदों में कोई सार्व गुणनखंड नहीं है। हम किस प्रकार प्रारंभ करेंगे?
आइए, (2xy + 2y) को गुणनखंड रूप में लिखें।
2xy + 2y = (2 × x × y) + (2 × y)
= (2 × y × x) + (2 × y × 1)
= (2y × x) + (2y × 1) = 2y (x + 1)
इसी प्रकार, 3x + 3 = (3 × x) + (3 × 1)
= 3 × (x + 1) = 3 ( x + 1)
अतः 2xy + 2y + 3x + 3 = 2y (x + 1) + 3 (x +1)
ध्यान दीजिए कि यहाँ दाएँ पक्ष के दोनों पदों में एक सार्व गुणनखंड (x + 1) है। दोनों पदों को मिलाने पर,
2xy + 2y + 3x + 3 = 2y (x + 1) + 3 (x + 1) = (x + 1) (2y + 3)
अब, व्यंजक 2xy + 2y + 3x + 3 गुणनखंडों के गुणनफल के रूप में है। इसके गुणनखंड (x + 1) और (2x + 3) हैं। ध्यान दीजिए कि ये गुणनखंड अखंडनीय हैं।

मान लीजिए कि उपरोक्त व्यंजक 2xy + 3 + 2y + 3x के रूप में दिया है, तब इसका गुणनखंडन देखना सरल नहीं है। इसी व्यंजक को 2xy + 2y + 3x + 3 के रूप में पुनर्व्यवस्थित करने पर,
इसके (2xy + 2y) और (3x + 3) समूह बनाकर गुणनखंडन किया जा सकता है, यही पुनः समूहन है।