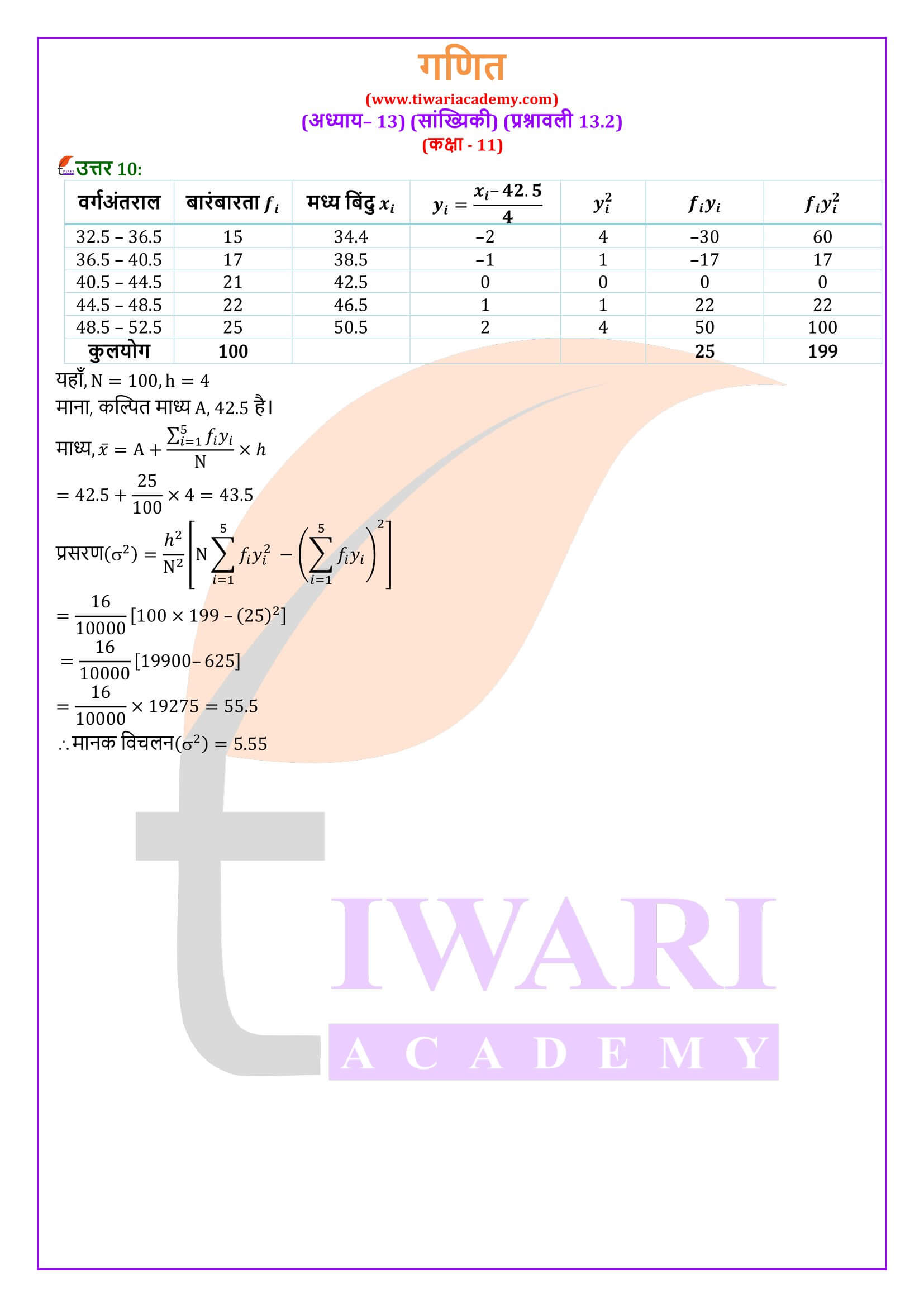
एनसीईआरटी समाधान कक्षा 11 गणित प्रश्नावली 13.2

हम जानते हैं कि आँकड़ों को दो प्रकार से वर्गीकृत किया जाता है।
(a) असतत बारंबारता बंटन
(b) सतत बारंबारता बंटन
मान लीजिए कि दिए गए आँकड़ों में n भिन्न प्रेक्षण x₁, x₂, …, xₙ हैं
जिनकी बारंबारताएं क्रमशः f₁, f₂, …, fₙ हैं। इन आँकड़ों को सारणीबद्ध रूप में निम्नलिखित प्रकार से व्यक्त किया जा सकता है जिसे असतत बारंबारता बंटन कहते हैंः
x: x₁, x₂, x₃, …, xₙ
f: f₁, f₂, f₃, …, fₙ

सर्वप्रथम हम दिए गए आँकड़ों का निम्नलिखित सूत्र द्वारा माध्य x̅ ज्ञात करते हैंः
x̅ = ∑_(i=1)^nxᵢfᵢ / ∑_(i=1)^nfᵢ
= 1/N ∑_(i=1)^nxᵢfᵢ
जहाँ ∑_(i=1)^nxᵢfᵢ प्रेक्षणों xᵢ का उनकी क्रमशः बारंबारता fᵢ से गुणनफलों का योग प्रकट करता है। तथा N = ∑_(i=1)^nfᵢ बारंबारताओं का योग है।
तब हम प्रेक्षणों xᵢ का माध्य x̅ से विचलन ज्ञात करते हैं और उनका निरपेक्ष मान लेते हैं अर्थात सभी i =1, 2, …, n के लिए xᵢ – x̅ ज्ञात करते हैं।
इसके पश्चात् विचलनों के निरपेक्ष मान का माध्य ज्ञात करते हैं, जोकि माध्य के सापेक्ष वांछित माध्य विचलन है।
x̅ = ∑_(i=1)^n〖।xᵢ-x̅।fᵢ〗 / ∑_(i=1)^nfᵢ
= 1/N ∑_(i=1)^n〖।xᵢ-x̅।fᵢ〗

बहुत अधिक विचरण या बिखराव वाली शृंखलाओं में माध्यिका केंद्रीय प्रवृत्ति की उपयुक्त माप नहीं होती है। अतः इस दशा में माध्यिका के सापेक्ष माध्य विचलन पर पूरी तरह विश्वास नहीं किया जा सकता है।

केंद्रीय प्रवृत्ति की माप के सापेक्ष माध्य विचलन ज्ञात करने के लिए हमने विचलनों के निरपेक्ष मानों का योग किया था। ऐसा माध्य विचलन को सार्थक बनाने के लिए किया था, अन्यथा विचलनों का योग शून्य हो जाता है।
विचलनों के चिह्नों के कारण उत्पन्न इस समस्या को विचलनों के वर्ग लेकर भी दूर किया जा सकता है। निसंदेह यह स्पष्ट है कि विचलनों के यह वर्ग ऋणेतर होते हैं।

माना x₁, x₂, …, xₙ, n प्रेक्षण हैं तथा x̅ उनका माध्य है। तब
(x₁ – x̅)² + (x₂ – x̅)² + …. + (xₙ – x̅)² = ∑_(i=1)^n〖(xᵢ – x̅)²〗
यदि यह योग शून्य हो तो प्रत्येक यदि यह योग शून्य हो तो प्रत्येक (xᵢ – x̅) शून्य हो जाएगा। इसका अर्थ है कि किसी प्रकार का विचरण नहीं है क्योंकि तब सभी प्रेक्षण x̅ के बराबर हो जाते हैं।
यदि ∑_(i=1)^n〖(xᵢ – x̅)²〗= छोटा है तो यह इंगित करता है कि प्रेक्षण x₁, x₂, …, xₙ, माध्य x̅ के निकट हैं तथा प्रेक्षणों का माध्य x̅ के सापेक्ष विचरण कम है । इसके विपरीत यदि यह योग बड़ा है तो प्रेक्षणों का माध्य x̅ के सापेक्ष विचरण अधिक है।