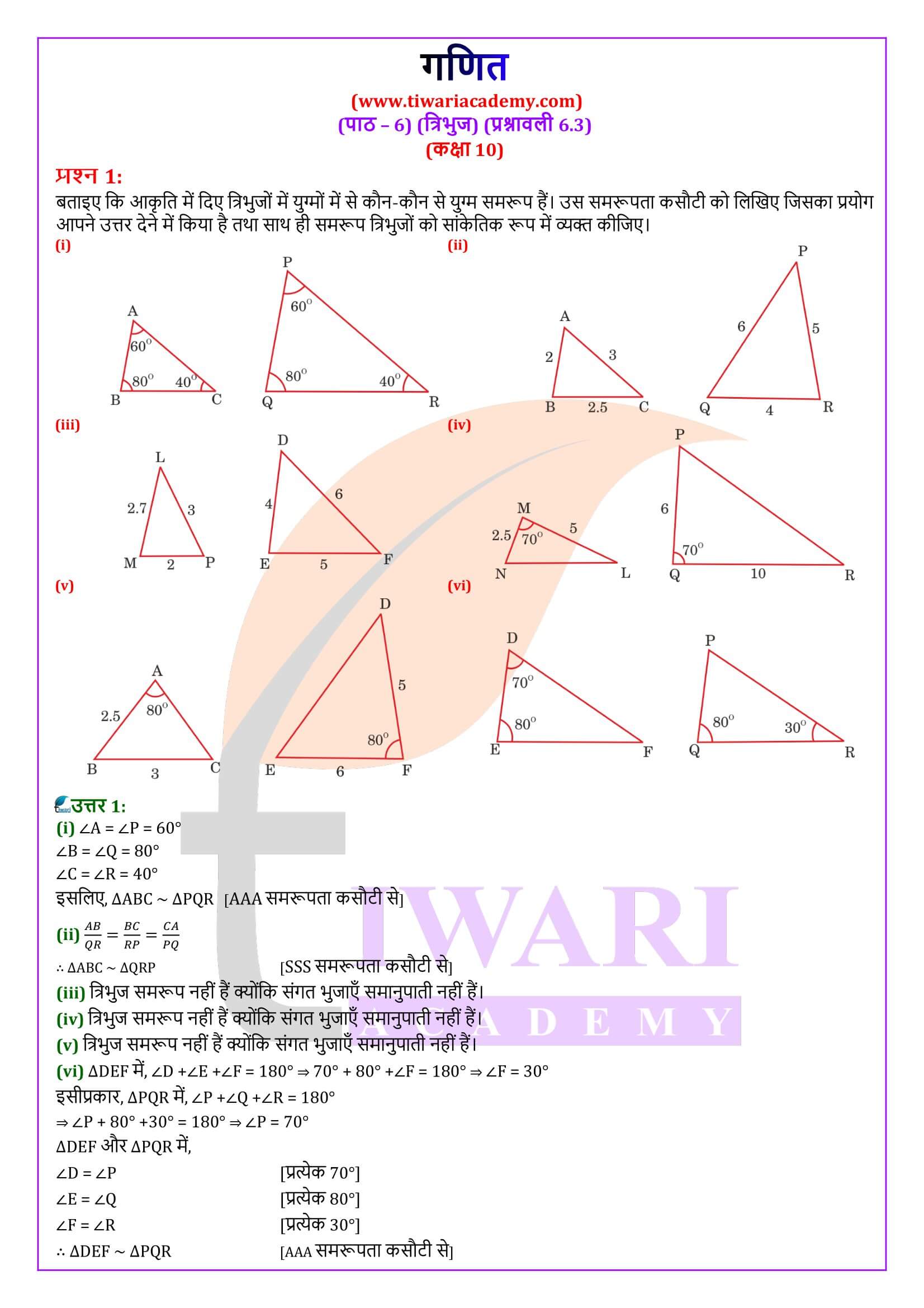
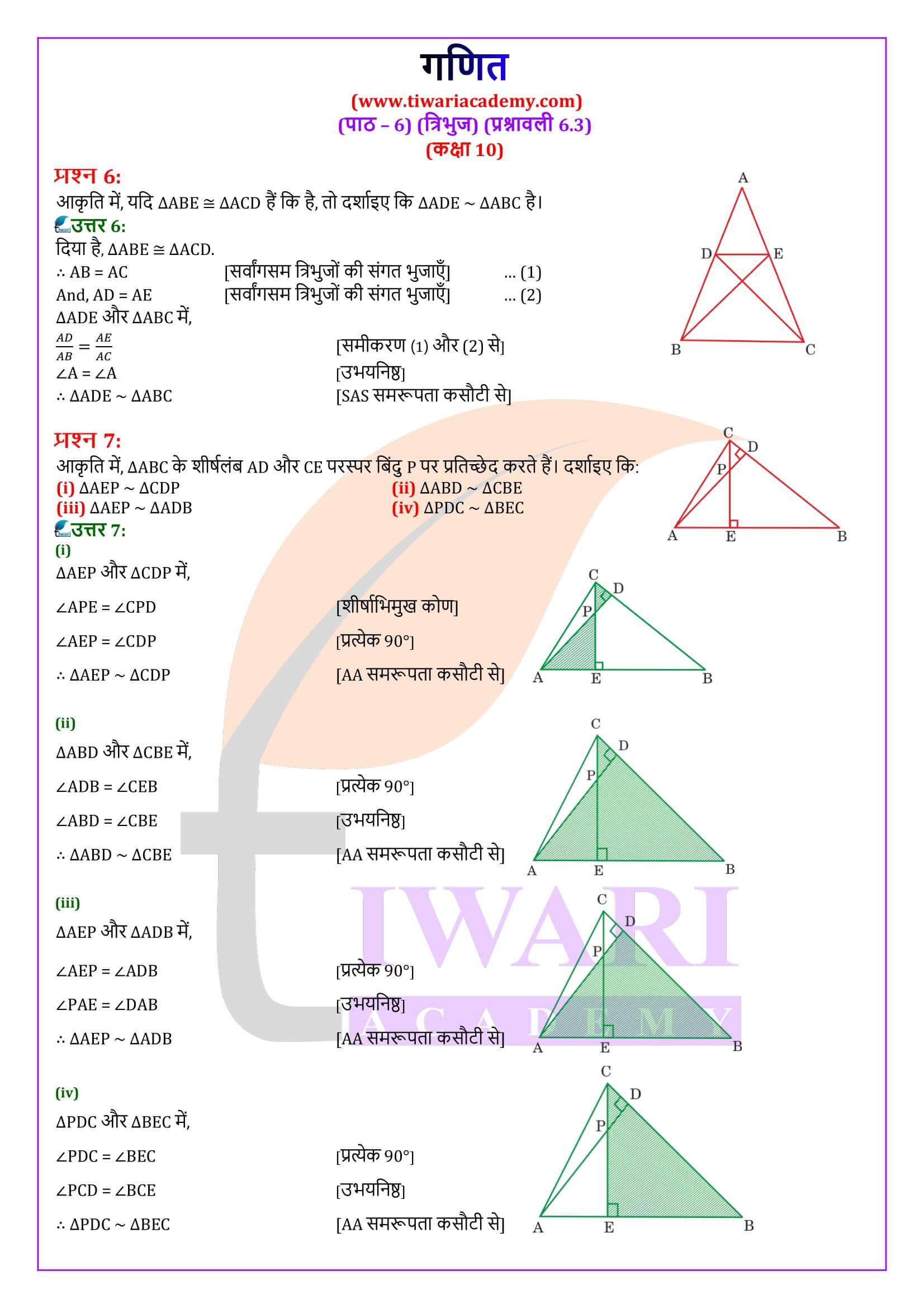
एनसीईआरटी समाधान कक्षा 10 गणित प्रश्नावली 6.3

दो त्रिभुज समरूप होते हैं यदि:
(i) उनके संगत कोण बराबर हों तथा
(ii) उनकी संगत भुजाएँ एक ही अनुपात में (समानुपाती हों)।
अर्थात् यदि ∆ ABC और ∆ DEF में
(i) ∠A = ∠D, ∠B = ∠E, ∠C = ∠F है तथा
(ii) AB/DE = BC/EF = CA/FD
यहाँ आप देख सकते हैं कि A, D के संगत है B, E के संगत है तथा C, F के संगत है। सांकेतिक रूप से, हम इन त्रिभुजों की समरूपता को ‘∆ ABC ~ ∆ DEF’ लिखते हैं तथा ‘त्रिभुज ABC समरूप है त्रिभुज DEF के’ पढ़ते हैं। संकेत ‘~’ ‘समरूप’ को प्रकट करता है।

इस प्रमेय को सिद्ध किया जा सकता है, यदि हम एक रेखा DE इस प्रकार लें कि AB/DB = AE/EC हो तथा DE भुजा BC के समान्तर न हो।
अब यदि DE भुजा BC के समांतर नहीं है, तो BC के समांतर एक रेखा DE’ खींचिए।
अतः AD/DB = AE’/E’C
इसलिए, AE/EC = AE’/E’C
उपरोक्त के दोनों पक्षों में 1 जोड़ कर, आप यह देख सकते हैं कि E और E’ को अवश्य ही संपाती होना चाहिए।
एक उदाहरण के माध्यम से उपरोक्त प्रमेय का प्रयोग स्पष्ट करते हैं।

यदि कोई रेखा एक ∆ ABC की भुजाओं AB और AC को क्रमशः D और E पर प्रतिच्छेद करे तथा भुजा BC के समांतर हो, तो सिद्ध कीजिए कि
AD/AB = AE/AC होगा।
हल:
DE || BC (दिया है)
अतः AD/DB = AE/EC (प्रमेय 6.1)
अर्थात् DB/AD = EC/AE
या DB/AD + 1 = EC/AE + 1
या AB/AD = AC/AE
अतः AD/AB = AE/AC

1. यदि दो त्रिभुजों में, संगत कोण बराबर हों, तो उनकी संगत भुजाएँ एक ही अनुपात में होती हैं और इसीलिए दोनों त्रिभुज समरूप होते हैं। (AAA समरूपता कसौटी)
2. यदि दो त्रिभुजों में, एक त्रिभुज के दो कोण क्रमशः दूसरे त्रिभुज के दो कोणों के बराबर हों, तो दोनों त्रिभुज समरूप होते हैं। (AA समरूपता कसौटी)
3. यदि दो त्रिभुजों में, संगत भुजाएँ एक ही अनुपात में हों, तो उनके संगत कोण बराबर होते हैं और इसीलिए दोनों त्रिभुज समरूप होते हैं। (SSS समरूपता कसौटी)