एनसीईआरटी समाधान कक्षा 10 गणित प्रश्नावली 6.2

त्रिभुज भी एक बहुभुज ही है। इसलिए, हम त्रिभुजों की समरूपता के लिए भी वही प्रतिबंध लिख सकते हैं, जो बहुभुजों की समरूपता के लिए लिखे थे।
अर्थात्
दो त्रिभुज समरूप होते हैं, यदि:

• (i) उनके संगत कोण बराबर हों तथा
• (ii) उनकी संगत भुजाएँ एक ही अनुपात में (अर्थात् समानुपाती) हों।

यदि दो त्रिभुजों के संगत कोण बराबर हों, तो वे समानकोणिक त्रिभुज कहलाते हैं।

नोट
प्रसिद्ध यूनानी गणितज्ञ थेल्स ने दो समानकोणिक त्रिभुजों से संबंधित एक महत्वपूर्ण तथ्य प्रतिपादित किया, जो नीचे दिया जा रहा हैः
दो समानकोणिक त्रिभुजों में उनकी संगत भुजाओं का अनुपात सदैव समान रहता है।

यदि किसी त्रिभुज की एक भुजा के समांतर अन्य दो भुजाओं को भिन्न-भिन्न बिदुओं पर प्रतिच्छेद करने के लिए एक रेखा खींची जाए, तो ये अन्य दो भुजाएँ एक ही अनुपात में विभाजित हो जाती हैं।

उपपत्ति:
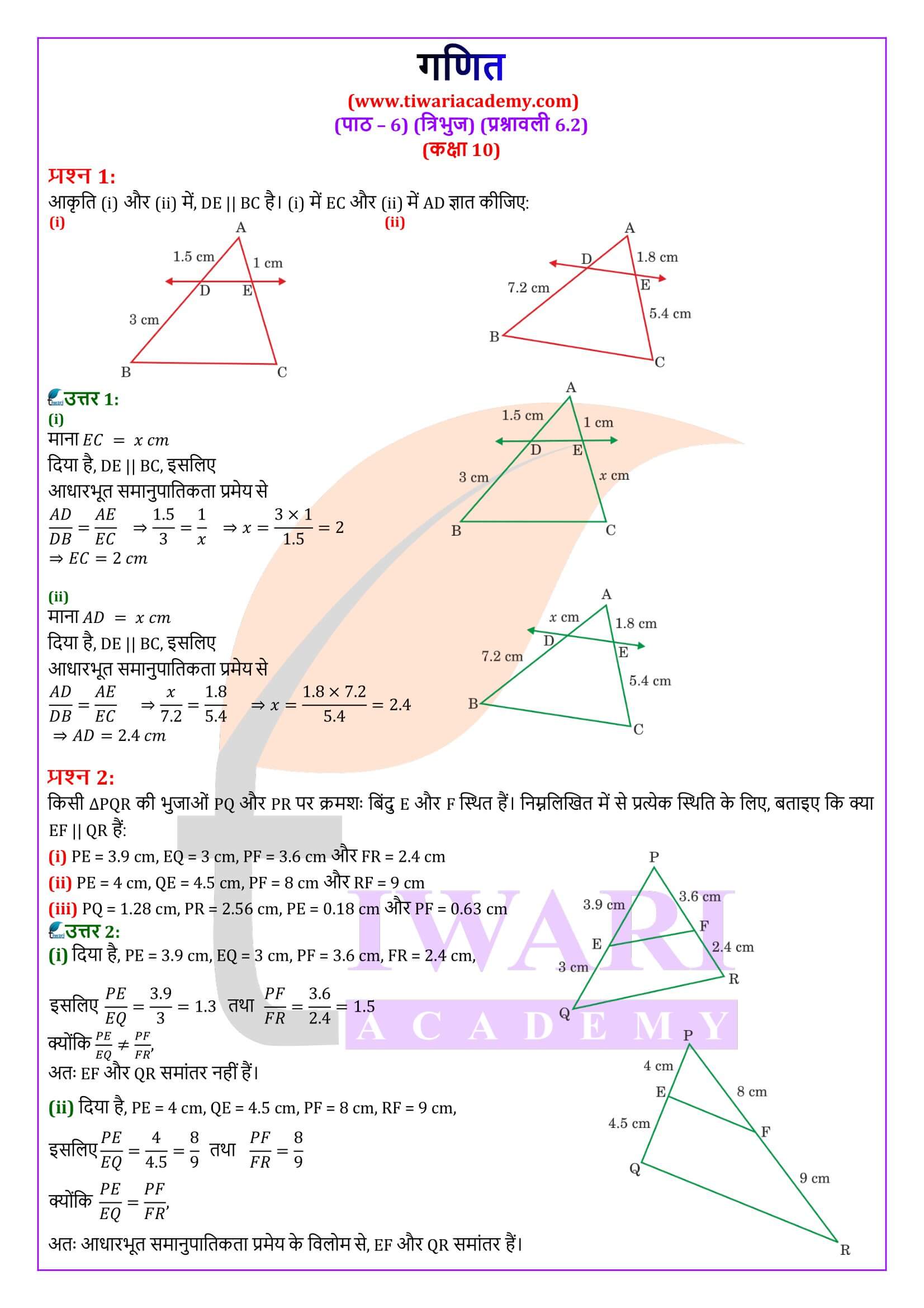
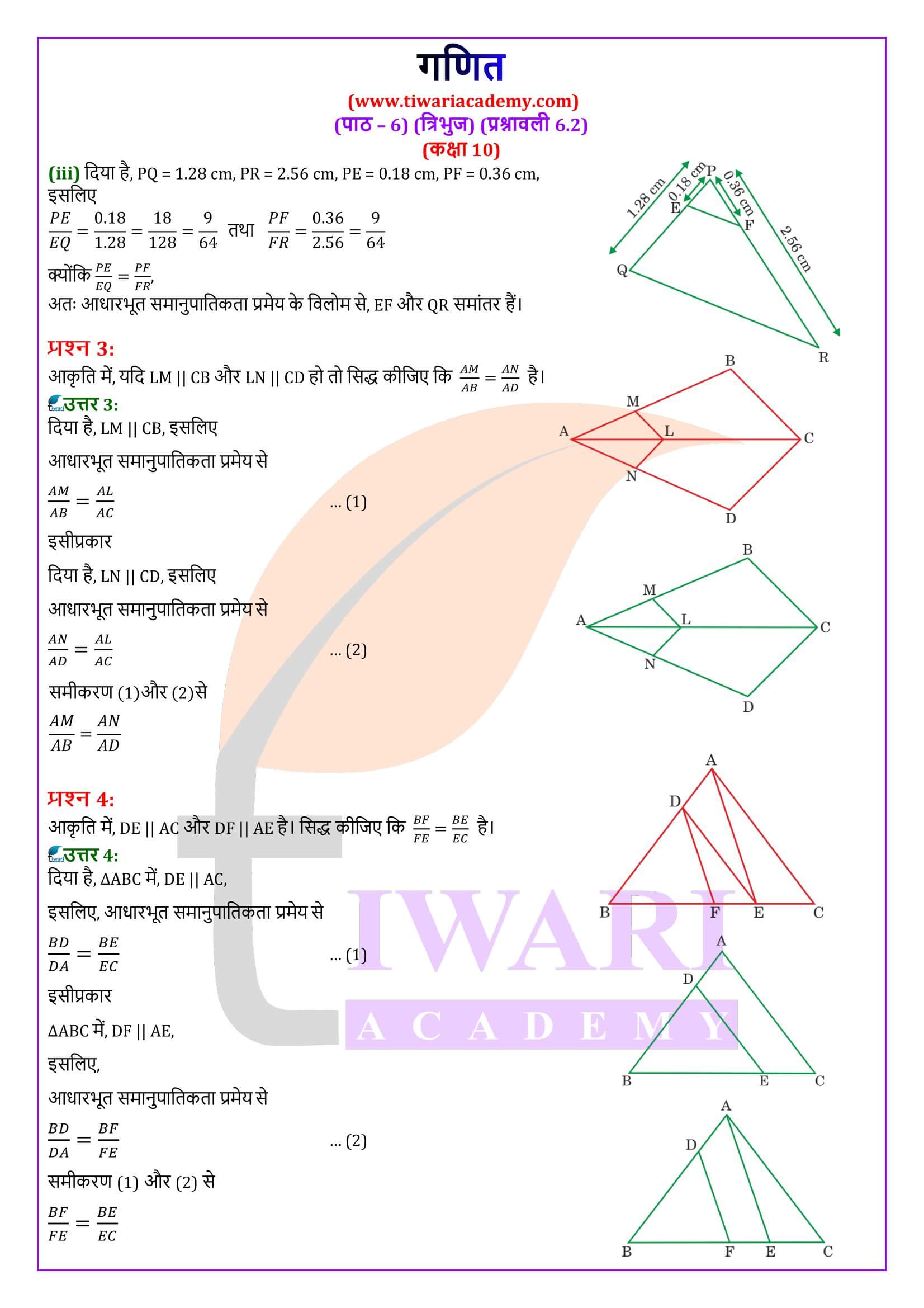
हमें एक त्रिभुज ABC दिया है, जिसमें भुजा BC के समांतर खींची गई एक रेखा अन्य दो भुजाओं AB और AC को क्रमशः D और E पर काटती हैं।
हमें सिद्ध करना है कि AD/DB = AE/EC
आइए B और E तथा C और D को मिलाएँ और फिर DM ⊥ AC, एवं EN ⊥ AB खीचें।
अब ∆ ADE का क्षेत्रफल = 1/2(आधार × ऊंचाई) = ½ × AD × EN = ½ × AE × DM
इसी प्रकार ∆ BDE का क्षेत्रफल = ½ × DB × EN
∆ DEC का क्षेत्रफल = ½ × DM × EC
अतः (∆ ADE का क्षेत्रफल) / ∆ BDE का क्षेत्रफल = (½ × AD × EN) / (½ × DB × EN)
= AD/ DB (1)
तथा (∆ ADE का क्षेत्रफल) / ∆ DEC का क्षेत्रफल = (½ × AE × DM) / (½ × DM × EC)
= AE / EC (2)
यहाँ पर ∆ BDE और ∆ DEC एक ही आधार DE और समान्तर रेखाओं BC और DE के बीच बने दो त्रिभुज हैं।
अतः ∆ BDE का क्षेत्रफल = ∆ DEC का क्षेत्रफल (3)
इसलिए समीकरण 1, 2 और 3 से प्राप्त होता है
AD/ DB = AE / EC

1. यदि किसी त्रिभुज की एक भुजा के समांतर अन्य दो भुजाओं को भिन्न-भिन्न बिदुओं पर प्रतिच्छेद करने के लिए, एक रेखा खींची जाए, तो ये अन्य दो भुजाएँ एक ही अनुपात में विभाजित हो जाती हैं।
2. यदि एक रेखा किसी त्रिभुज की दो भुजाओं को एक ही अनुपात में विभाजित करे, तो यह रेखा तीसरी भुजा के समांतर होती है।