एनसीईआरटी समाधान कक्षा 10 गणित प्रश्नावली 6.1

तीन रेखाखण्डों से घिरी हुई समतलीय आकृति त्रिभुज कहलाती है। त्रिभुज को ∆ से निरूपित किया जाता है। एक त्रिभुज की तीन भुजाएँ, तीन कोण और तीन शीर्ष होते हैं। त्रिभुज के तीनों कोणों का योग 180° होता है।

त्रिभुजों का वर्गीकरण निम्नलिखित दो आधार पर किया जा सकता है:

• (i) भुजाओं के आधार पर
• (ii) कोणों के आधार पर

भुजाओं के आधार पर त्रिभुज तीन प्रकार के होते हैं:

• (i) विषमबाहु त्रिभुज
• (ii) समद्विबाहु त्रिभुज
• (iii) समबाहु त्रिभुज

कोणों के आधार पर त्रिभुज तीन प्रकार के होते हैं:
(i) न्यून कोण त्रिभुज
(ii) अधिक कोण त्रिभुज
(iii) समकोण त्रिभुज
उपरोक्त चर्चा से, हम यह भी कह सकते हैं कि सभी सर्वांगसम आकृतियाँ समरूप होती हैं, परंतु सभी समरूप आकृतियों का सर्वांगसम होना आवश्यक नहीं है।
सर्वांगसम त्रिभुज
जब दो त्रिभुज की सारी भुजाओं एवं कोणों का माप समान होता है तो वे त्रिभुज सर्वांगसम होते हैं।

दो त्रिभुज समरूप होंगे यदि
(i) यदि दो त्रिभुजों में, संगत कोण समान हों, तो त्रिभुज समरूप होते हैं।
(ii) यदि दो त्रिभुजों की संगत भुजाएँ समानुपाती हों, तो त्रिभुज समरूप होते हैं।
(iii) यदि एक त्रिभुज का एक कोण दूसरे त्रिभुज के एक कोण के बराबर हो तथा उन कोणों को बनाने वाली भुजाएँ समानुपाती हों, तो त्रिभुज समरूप होते हैं।

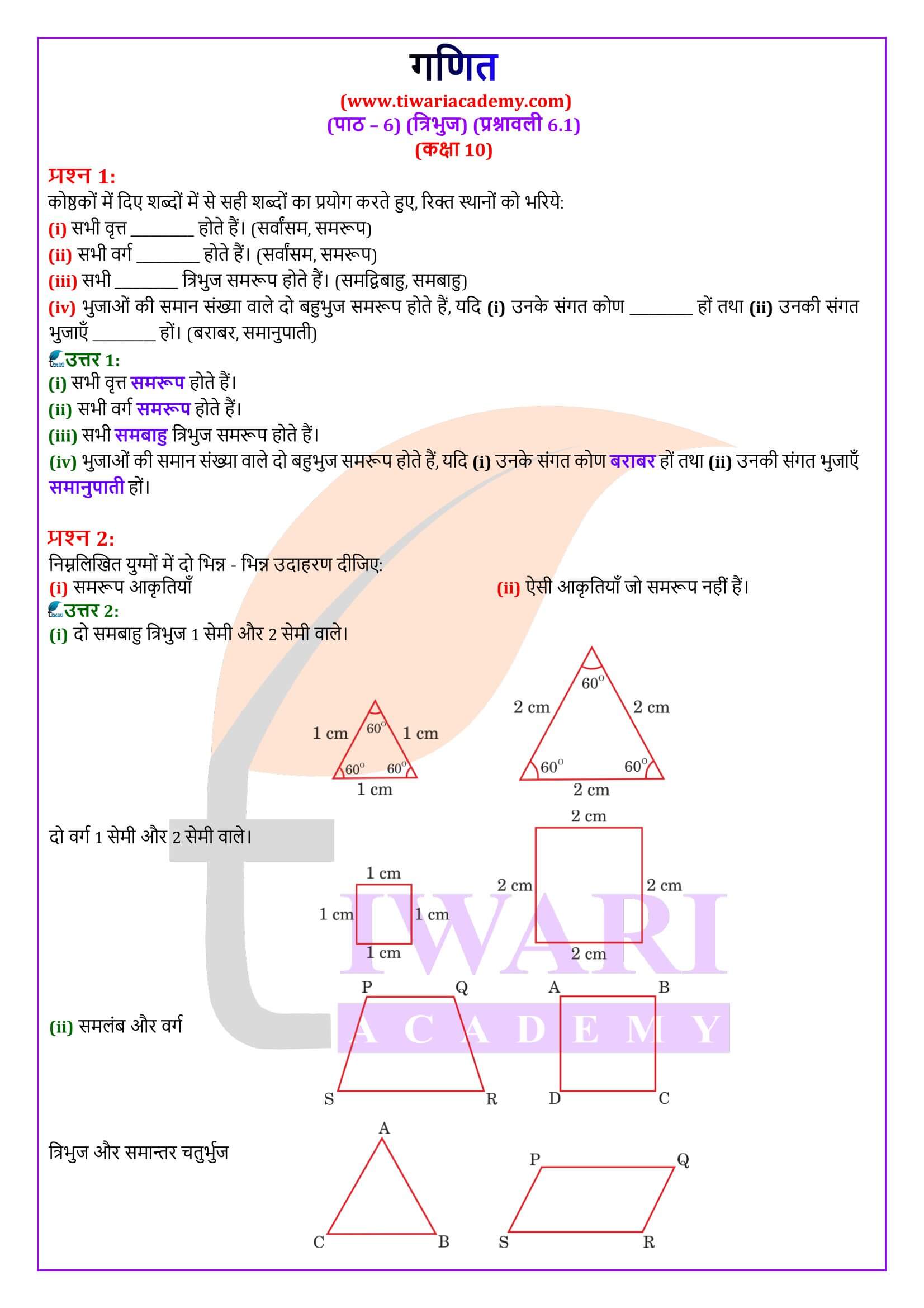
कोष्ठकों में दिए शब्दों में से सही शब्दों का प्रयोग करते हुए, रिक्त स्थानों को भरिएः
(i) सभी वृत्त ____________ होते हैं। (सर्वांगसम, समरूप)
(ii) सभी वर्ग ____________ होते हैं। (समरूप, सर्वांगसम)
(iii) सभी त्रिभुज ___________ समरूप होते हैं। (समद्विबाहु, समबाहु)
(iv) भुजाओं की समान संख्या वाले दो बहुभुज समरूप होते हैं, यदि उनके संगत कोण _________ हों तथा उनकी संगत भुजाएँ ______हों। (बराबर, समानुपाती)
उत्तर:
(i) समरूप
(ii) समरूप
(iii) समबाहु
(iv) बराबर, समानुपाती

(i) AAS (कोण-कोण-भुजा):
यदि दो त्रिभुजों के कोणों के दो युग्म माप में बराबर हों, और संगत गैर-शामिल भुजाओं का एक युग्म लंबाई में बराबर हो, तो त्रिभुज सर्वांगसम होते हैं। …
(ii) RHS (समकोण-कर्ण-पक्ष):
यदि दो समकोण त्रिभुजों के कर्णों की लंबाई समान है, और छोटी भुजाओं का एक युग्म लंबाई में समान है, तो त्रिभुज सर्वांगसम होते हैं।

कोणों के आधार पर त्रिभुज तीन प्रकार के होते हैं:
न्यून कोण त्रिभुज: (उस त्रिभुज को कहते हैं जिसके तीनों कोण, न्यूनकोण (90° से कम) हों।)
अधिक कोण त्रिभुज: (उस त्रिभुज को कहते हैं जिसका कोई एक कोण, अधिककोण (90° से अधिक) हो।)
समकोण त्रिभुज: (जिसका एक कोण 90 अंश का (अर्थात, समकोण) हो।)