एनसीईआरटी समाधान कक्षा 10 गणित प्रश्नावली 13.3
एनसीईआरटी समाधान कक्षा 10 गणित प्रश्नावली 13.3 सांख्यिकी के अभ्यास के उत्तर हिंदी में सीबीएसई और राजकीय बोर्ड सत्र 2025-26 के लिए यहाँ से प्राप्त किए जा सकते हैं। प्रत्येक प्रश्न को चरण दर चरण हल किया गया है। प्रश्नों को विडियो के माध्यम से भी हल करके दिखाया गया है ताकि प्रत्येक विद्यार्थी इसे आसानी से समझ सके।
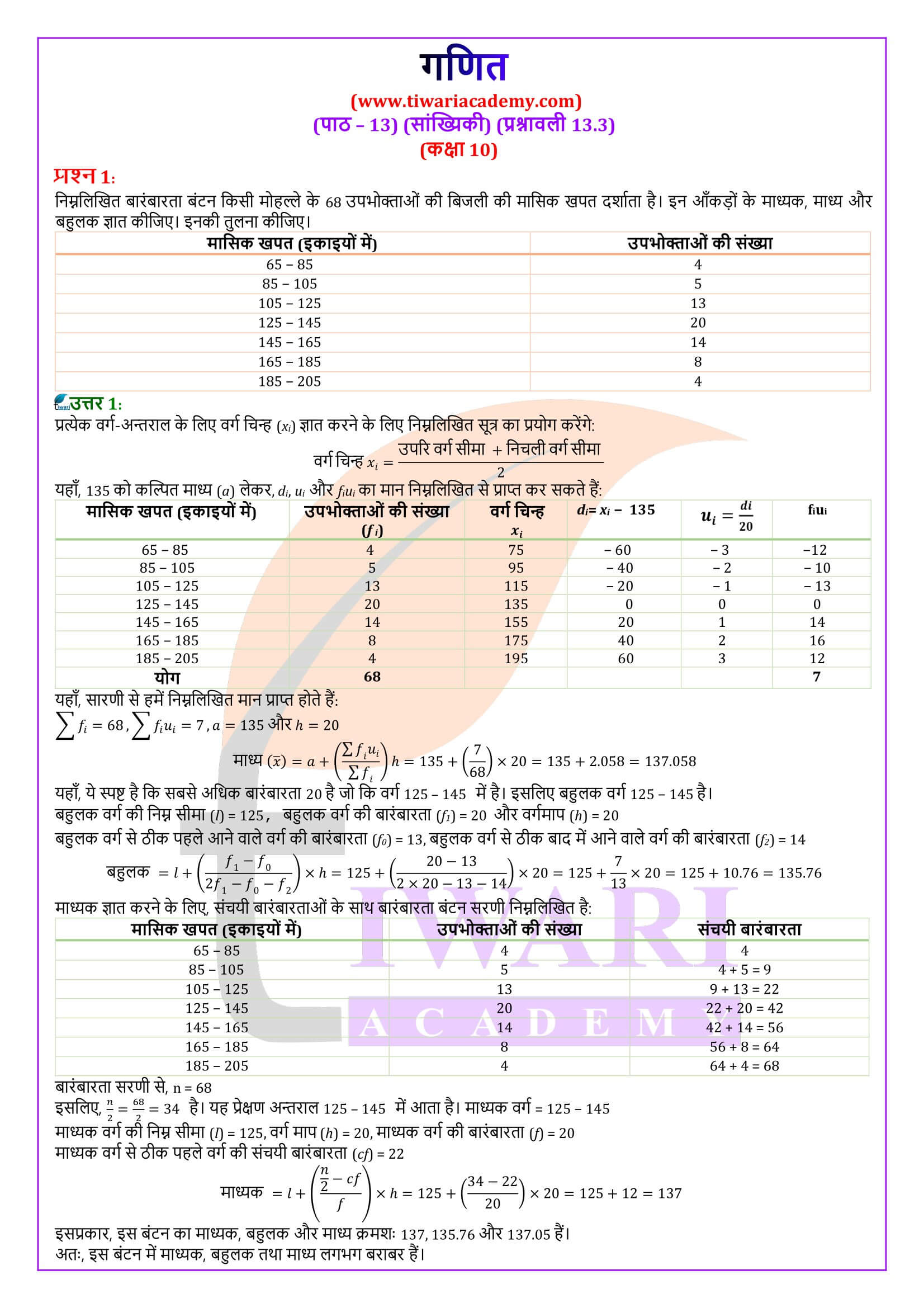
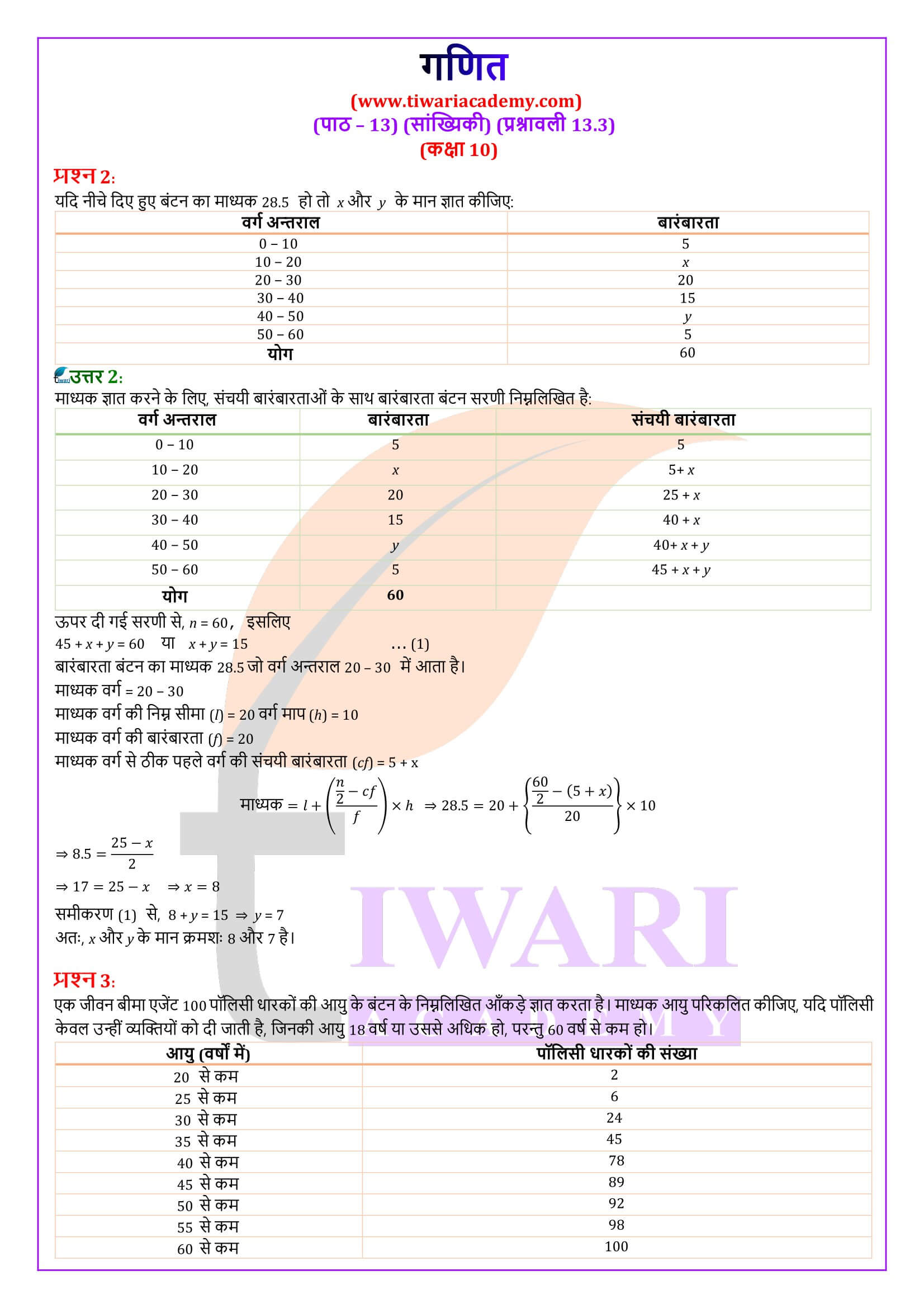
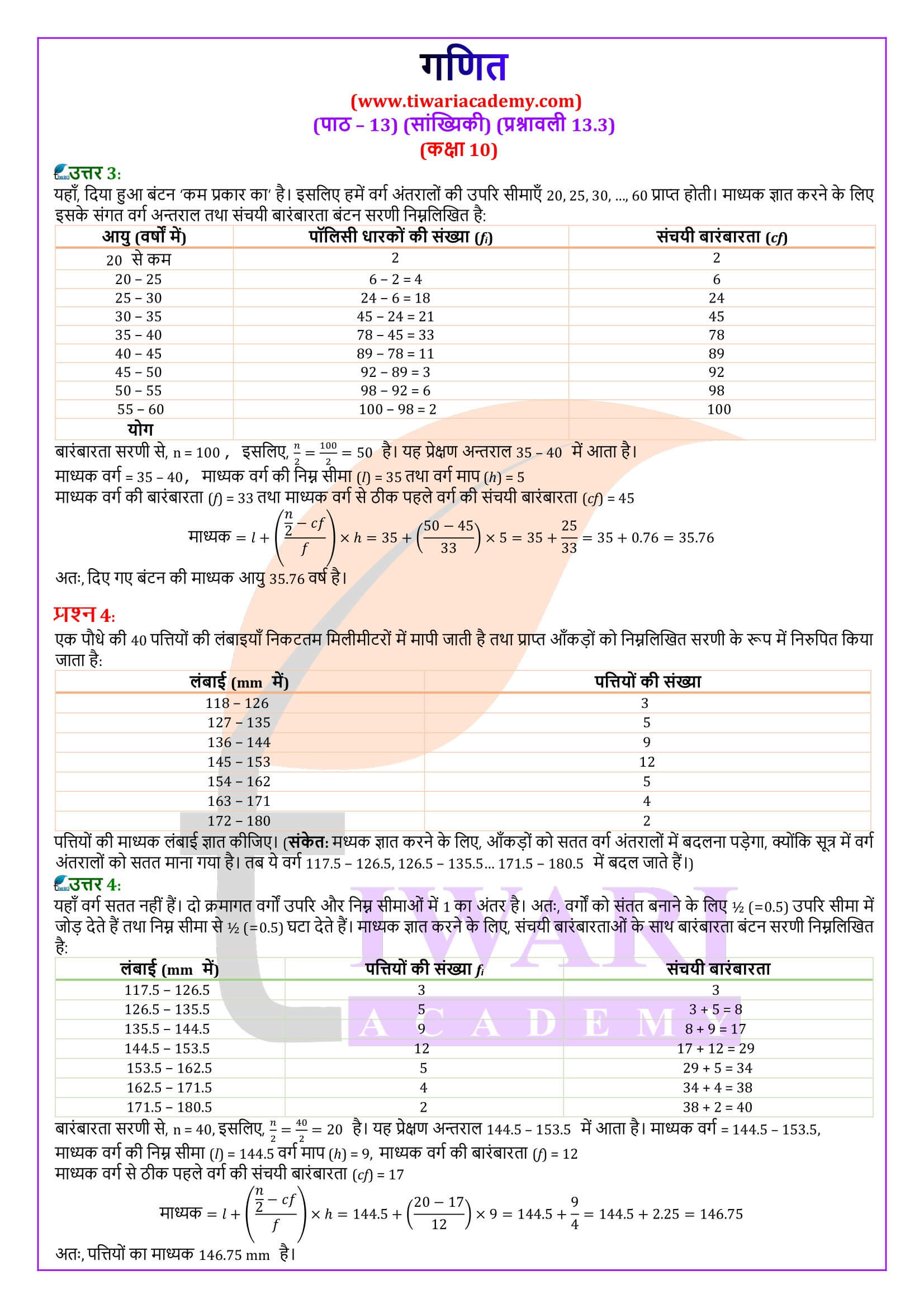
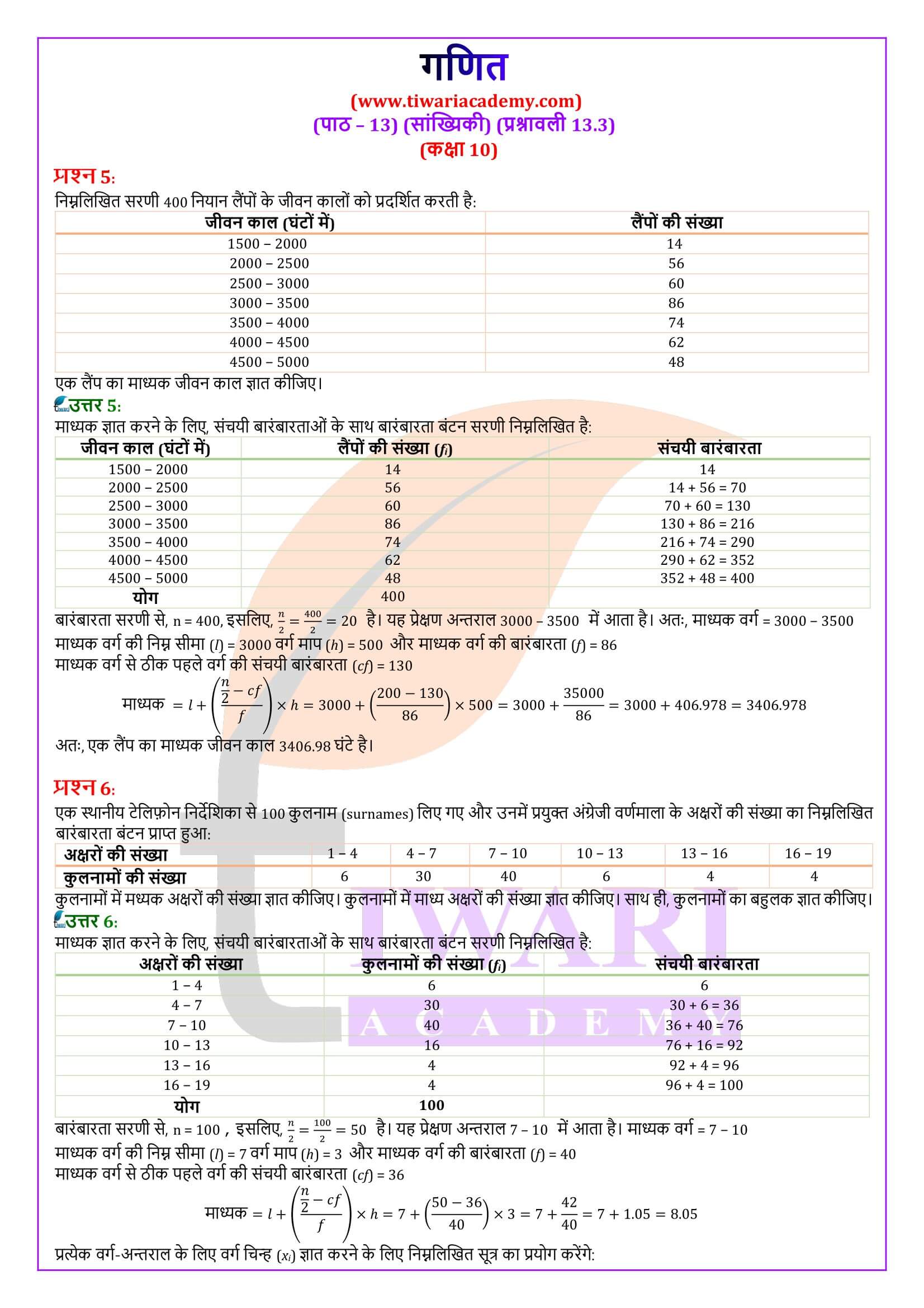
एनसीईआरटी समाधान कक्षा 10 गणित प्रश्नावली 13.3
कक्षा 10 गणित अध्याय 13 प्रश्नावली 13.3 के लिए एनसीईआरटी समाधान
वर्गीकृत आंकड़ों का बहुलक
बहुलक दिए हुए प्रेक्षणों में वह मान है जो सबसे अधिक बार आता है, अर्थात् उस प्रेक्षण का मान जिसकी बारंबारता अधिकतम है।
उदाहरण:
किसी गेंदबाज़ द्वारा 10 क्रिकेट मैचों में लिए गए विकिटों की संख्याएँ निम्नलिखित हैं:
2, 6, 4, 5, 0, 2, 1, 3, 2, 3
इन आँकड़ों का बहुलक ज्ञात कीजिए।
ऊपर दिए गए प्रश्न का हल
आइए उपरोक्त आँकड़ों के लिए, एक बारंबारता बंटन सारणी बनाएँ, जैसा कि नीचे दर्शाया गया है:
विकेटों की संख्या क्रिकेट मैचों की संख्या
0 1
1 1
2 3
3 2
4 1
5 1
6 1
स्पष्ट है कि गेंदबाज़ ने अधिकतम मैचों (3) में 2 विकिट लिए हैं। अतः, इन आँकड़ों का बहुलक 2 है।
बहुलक वर्ग
एक वर्गीकृत बारंबारता बंटन में, बारंबारताओं को देखकर बहुलक ज्ञात करना संभव नहीं है। यहाँ, हम केवल वह वर्ग ज्ञात कर सकते हैं जिसकी बारंबारता अधिकतम है। इस वर्ग को बहुलक वर्ग कहते हैं। बहुलक इस बहुलक वर्ग के अंदर कोई मान है, जिसे निम्नलिखित सूत्र द्वारा ज्ञात किया जाता है:
बहुलक = l + (f₁ – f₀)/(2f₁ – f₀ – f₂) × h
जहाँ l = बहुलक वर्ग की निम्न (निचली) सीमा
h = वर्ग अंतराल की माप (यह मानते हुए कि सभी अंतराल बराबर मापों के हैं)
f₁ = बहुलक वर्ग की बारंबारता
f₀ = बहुलक वर्ग से ठीक पहले वर्ग की बारंबारता तथा
f₂ = बहुलक वर्ग के ठीक बाद में आने वाले वर्ग की बारंबारता है।
बहुलक पर आधारित प्रश्न
विद्यार्थियों के एक समूह द्वारा एक मोहल्ले के 20 परिवारों पर किए गए सर्वेक्षण के परिणामस्वरूप विभिन्न परिवारों के सदस्यों की संख्या से संबंधित निम्नलिखित आँकड़े प्राप्त हुए:
परिवार माप परिवारों की संख्या
1 – 3 7
3 – 5 8
5 – 7 2
7 – 9 2
9 – 11 1
इन आँकड़ों का बहुलक ज्ञात कीजिए।
उपरोक्त प्रश्न का हल
यहाँ, अधिकतम वर्ग बारंबारता 8 है तथा इस बारंबारता का संगत वर्ग 3-5 है। अतः, बहुलक वर्ग 3-5 है।
अब, बहुलक वर्ग = 3 – 5, बहुलक वर्ग की निम्न सीमा (l) = 3 तथा वर्ग माप (h) = 2 है।
बहुलक वर्ग की बारंबारता (f₁) = 8
बहुलक वर्ग से ठीक पहले वाले वर्ग की बारंबारता (f₀) = 7 तथा
बहुलक वर्ग के ठीक बाद में आने वाले वर्ग की बारंबारता (f₂) = 2 है।
आइए इन मानों को सूत्र में प्रतिस्थापित करें। हमें प्राप्त होता है:
बहुलक = l + (f₁ – f₀)/(2f₁ – f₀ – f₂) × h
= 3 + (8 – 7)/(2 × 8 – 7 – 2) × 2
= 3 + 1/7 × 2
= 23/7 = 3.286
अतः, उपरोक्त आँकड़ों का बहुलक 3.286 है।