एनसीईआरटी समाधान कक्षा 10 गणित प्रश्नावली 13.2

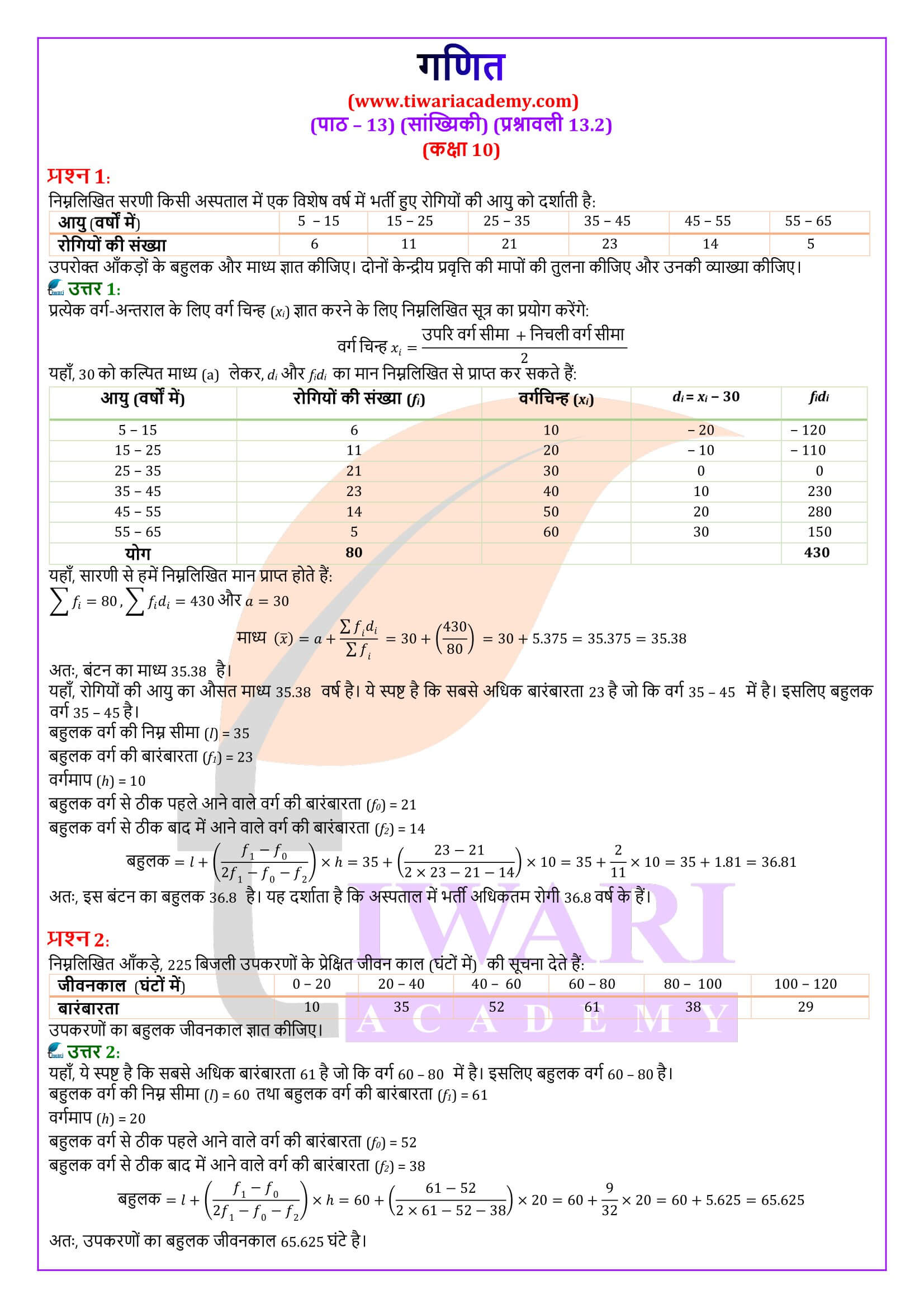
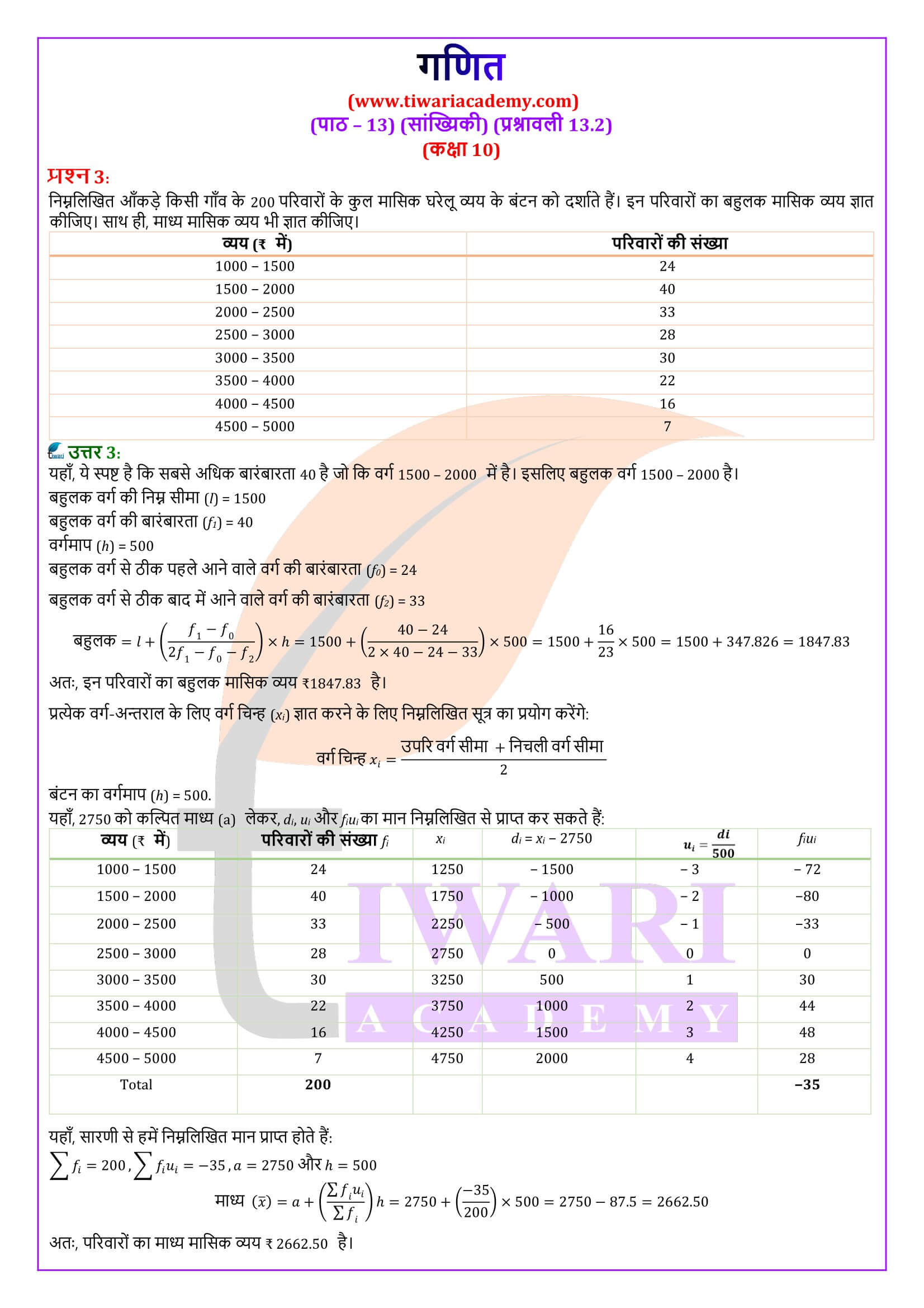
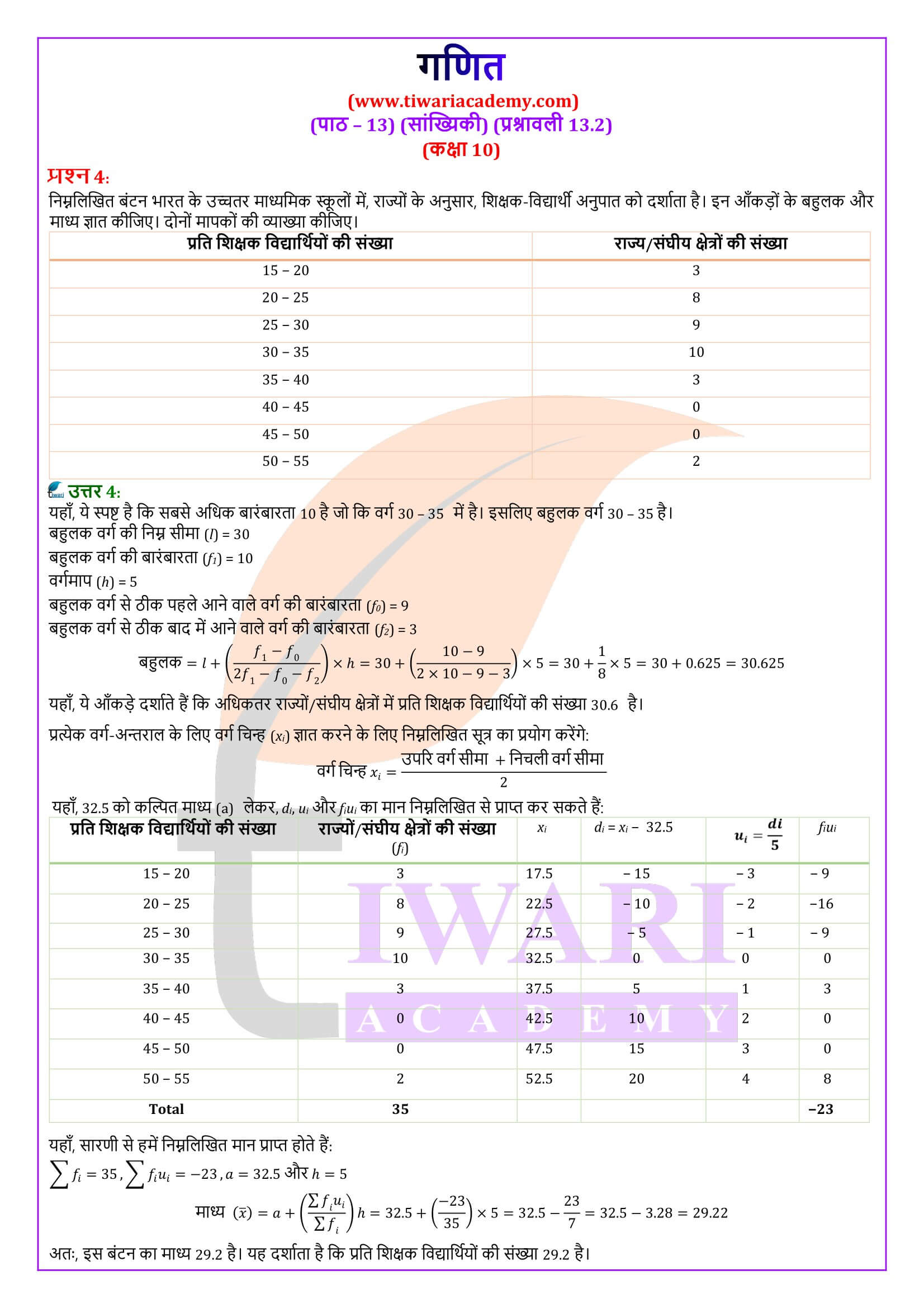
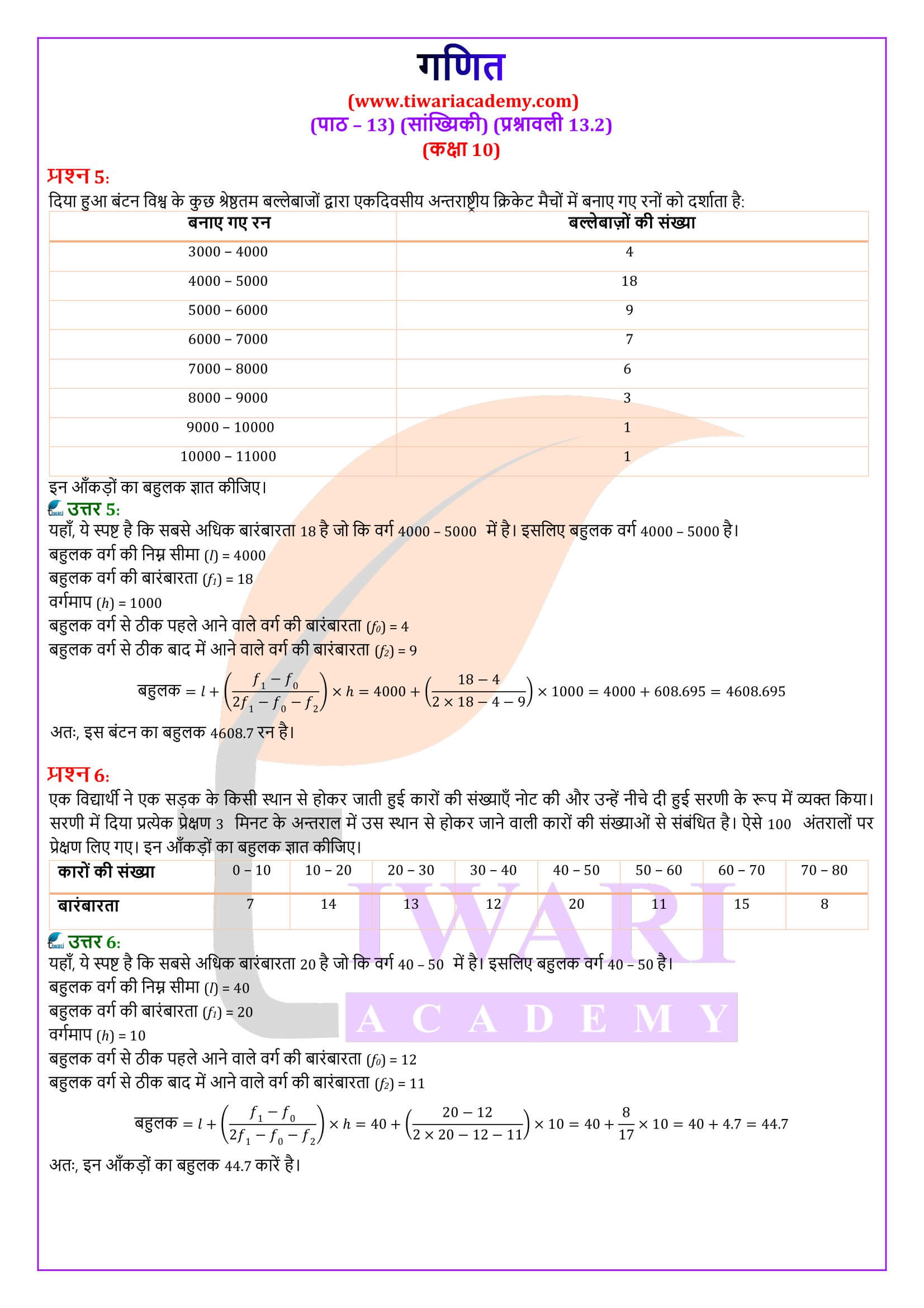
एनसीईआरटी पुस्तक के उदाहरण 1 के अवर्गीकृत आँकड़ों को चौड़ाई, मान लीजिए, 15 के वर्ग अंतराल बनाकर वर्गीकृत आँकड़ों में बदलें। याद रखिए कि वर्ग अंतरालों की बारंबारताएँ निर्दिष्ट करते समय, किसी उपरि वर्ग सीमा में आने वाले प्रेक्षण अगले वर्ग अंतराल में लिए जाते हैं। उदाहरणार्थ, अंक 40 प्राप्त करने वाले 4 विद्यार्थियों को वर्ग अंतराल 25-40 में न लेकर अंतराल 40-55 में लिया जाता है। इस परंपरा को ध्यान में रखते हुए, आइए इनकी एक वर्गीकृत बारंबारता सारणी बनाएँ:
वर्ग अंतराल विद्यार्थियों की संख्या
10 – 25 2
25 – 40 3
40 – 55 7
55 – 70 6
70 – 85 6
85 – 100 6

अब, प्रत्येक वर्ग अंतराल के लिए, हमें एक ऐसे बिदु (मान) की आवश्यकता है, जो पूरे अंतराल का प्रतिनिधित्व करे। यह मान लिया जाता है कि प्रत्येक वर्ग अंतराल की बारंबारता उसके मध्य-बिदु के चारों ओर केंद्रित होती है। अतः, प्रत्येक वर्ग के मध्य-बिंदु या वर्ग चिह्न को उस वर्ग में आने वाले सभी प्रेक्षणों का प्रतिनिधि माना जा सकता है। याद कीजिए कि हम एक वर्ग अंतराल का मध्य बिदु (या वर्ग चिह्न) उसकी उपरि और निचली सीमाओं का औसत निकालकर ज्ञात करते हैं। अर्थात्
वर्ग चिह्न = (उपरि वर्ग सीमा + निचली वर्ग सीमा)/2

उदाहरण के लिए वर्ग 10 – 25 के लिए वर्ग चिह्न xᵢ = (10 – 25)/2 = 17.5 है । इसी प्रकार अन्य वर्गों के लिए वर्ग चिह्न प्राप्त कर सकते हैं।
इससे हमें प्रत्येक वर्ग के लिए fᵢ xᵢ प्राप्त हो जायेगा।
अतः, दिए हुए आँकड़ों का माध्य x, नीचे दर्शाए अनुसार प्राप्त होता हैः
x = Σ fᵢxᵢ / Σ fᵢ = 1860/30
= 62
नोट: माध्य ज्ञात करने की इस नयी विधि को प्रत्यक्ष विधि कहा जा सकता है।

कभी-कभी जब xᵢ और fᵢ के मान बड़े होते हैं, तो xᵢ और fᵢ के गुणनफल ज्ञात करना जटिल हो जाता है तथा इसमें समय भी अधिक लगता है। अतः, ऐसी स्थितियों के लिए, आइए इन परिकलनों को सरल बनाने कल्पित माध्य विधि का सहारा लेते हैं। हम fᵢ के साथ कुछ नहीं कर सकते, परंतु हम प्रत्येक xᵢ को एक छोटी संख्या में बदल सकते हैं, जिससे हमारे परिकलन सरल हो जाएँगे।

इसमें पहला चरण यह हो सकता है कि प्राप्त किए गए सभी xᵢ में से किसी xᵢ को कल्पित माध्य के रूप में चुन लें तथा इसे “a” से व्यक्त करें। साथ ही, अपने परिकलन कार्य को और अधिक कम करने के लिए, हम “a” को ऐसा xᵢ ले सकते हैं जो x₁, x₂, ……….., xₙ के मध्य में कहीं आता हो। अतः, हम a = 47.5 या a = 62.5 चुन सकते हैं। आइए a = 47.5 चुनें।

अगला चरण है कि a और प्रत्येक xᵢ के बीच का अंतर dᵢ ज्ञात किया जाए, अर्थात् प्रत्येक xᵢ से “a” का विचलन ज्ञात किया जाए।
अर्थात् dᵢ = xᵢ – a
तीसरा चरण है कि प्रत्येक dᵢ और उसके संगत fᵢ का गुणनफल ज्ञात करके सभी fᵢ dᵢ का योग ज्ञात किया जाए।

विचलनों का माध्य d = Σ fᵢdᵢ / Σ fᵢ
या माध्य d = Σ fᵢ(xᵢ – a) / Σ fᵢ
अर्थात् x = a + Σ fᵢdᵢ / Σ fᵢ
नोट: माध्य ज्ञात करने की उपरोक्त विधि कल्पित माध्य विधि कहलाती है।