एनसीईआरटी समाधान कक्षा 11 गणित प्रश्नावली 13.1

सांख्यिकी गणित की वह शाखा है जिसमें आँकड़ों का संग्रहण, प्रदर्शन, वर्गीकरण और उसके गुणों का आकलन का अध्ययन किया जाता है। सांख्यिकी एक गणितीय विज्ञान है जिसमें किसी वस्तु/अवयव/तंत्र/समुदाय से सम्बन्धित आकड़ों का संग्रह, विश्लेषण, व्याख्या या स्पष्टीकरण और प्रस्तुति की जाती है।
उदाहरण:
दो बल्लेबाजों द्वारा पिछले दस मैचों में बनाए गए रनों पर विचार करेंः
बल्लेबाज A: 30, 91, 0, 64, 42, 80, 30, 5, 117, 71
बल्लेबाज B: 53, 46, 48, 50, 53, 53, 58, 60, 57, 52
स्पष्टतया आँकड़ों का माध्य व माध्यिका निम्नलिखित हैंः
बल्लेबाज A बल्लेबाज B
माध्य 53
माध्यिका 53

प्रेक्षणों का माध्य ( x̅ द्वारा निरूपित) उनके योग को उनकी संख्या से भाग देकर ज्ञात करते हैं।
अर्थात् x̅ = 1/n ∑_(i=1)^nxᵢ
माध्यिका की गणना के लिए आँकड़ों को पहले आरोही या अवरोही क्रम में व्यवस्थित किया जाता है और फिर निम्नलिखित नियम लगाया जाता हैः
यदि प्रेक्षणों की संख्या विषम है तो माध्यिका {(n + 1)/2} वाँ प्रेक्षण होती है। यदि प्रेक्षणों की संख्या सम है तो माध्यिका (n/2)वें और {(n/2) + 1} वें प्रेक्षणों का माध्य होती है।
आँकड़ों में प्रकीर्णन या विक्षेपण का माप प्रेक्षणों व वहाँ प्रयुक्त केंद्रीय प्रवृत्ति की माप के आधार पर किया जाता है।

(i) परिसर
(ii) चतुर्थक विचलन
(iii) माध्य विचलन
(iv) मानक विचलन

परिसर
प्रत्येक शृंखला के अधिकतम व न्यूनतम मूल्यों में अंतर प्राप्त करते हैं। इस अंतर को परिसर कहा जाता है।
एक शृंखला का परिसर = अधिकतम मान – न्यूनतम मान

किसी श्रृंखला के किसी माध्य के निकाले गए विचलनों के जोड़ के समांतर माध्य को माध्य विचलन कहा जाता है।
माध्य विचलन (a) = ‘a’ से विचलनों के निरपेक्ष मान का योग / प्रेक्षणों की संख्या
टिप्पणी:
माध्य विचलन केंद्रीय प्रवृत्ति की किसी भी माप से ज्ञात किया जा सकता है। किंतु सांख्यिकीय अध्ययन में सामान्यतः माध्य और माध्यिका के सापेक्ष माध्य विचलन का उपयोग किया जाता है।

मान लीजिए कि n प्रेक्षणों के आँकड़े x₁, x₂, x₃, …, xₙ दिए गए हैं। माध्य या माध्यिका के सापेक्ष माध्य विचलन की गणना में निम्नलिखित चरण प्रयुक्त होते हैंः
चरण-1: उस केंद्रीय प्रवृत्ति की माप को ज्ञात कीजिए जिससे हमें माध्य विचलन प्राप्त करना है। मान लीजिए यह “a” है।
चरण-2: प्रत्येक प्रेक्षण xᵢ का a से विचलन अर्थात् x₁ – a, x₂ – a, x₃ – a, ……., xₙ – a ज्ञात करें।
चरण-3: विचलनों का निरपेक्ष मान ज्ञात करें अर्थात् यदि विचलनों में ऋण चिह्न लगा है तो उसे हटा दें अर्थात् Ix₁ – aI, Ix₂ – aI, Ix₃ – aI, ….., Ixₙ – aI ज्ञात करें।
चरण-4: विचलनों के निरपेक्ष मानों का माध्य ज्ञात करें। यही माध्य ‘a’ के सापेक्ष माध्य विचलन है।
माध्य विचलन (a) = 1/n ∑_(i=1)^n〖।xᵢ-a।〗
अतः माध्य x̅ = 1/n ∑_(i=1)^n〖।xᵢ-x̅।〗
तथा माध्यिका M = 1/n ∑_(i=1)^n〖।xᵢ-M।〗

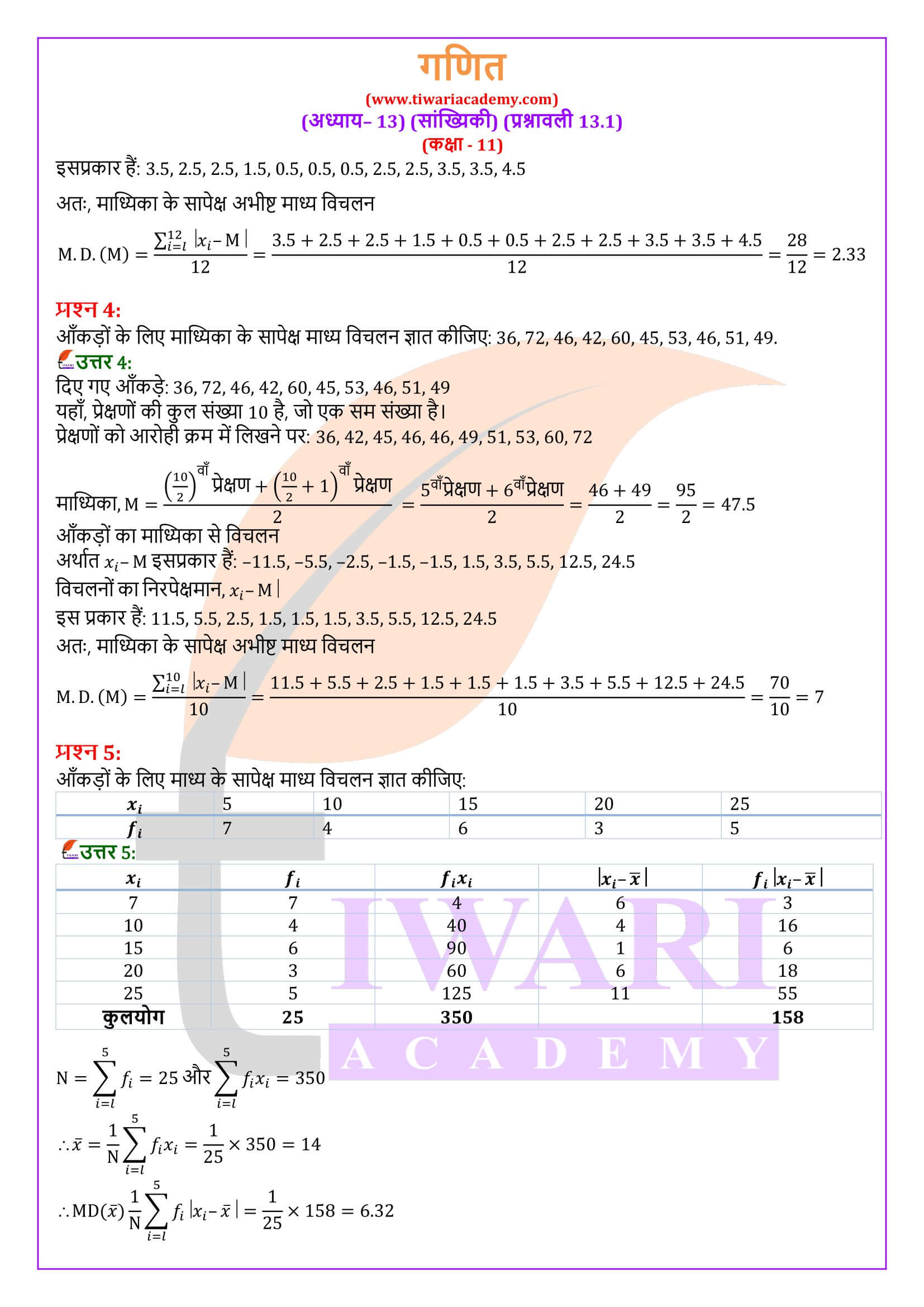
निम्नलिखित आँकड़ों के लिए माध्य के सापेक्ष माध्य विचलन ज्ञात कीजिएः
6, 7, 10, 12, 13, 4, 8, 12
हल:
हम क्रमबद्ध आगे बढ़ते हुए निम्नलिखित प्राप्त करते हैंः
चरण 1: दिए गए आँकड़ों का माध्य
x̅ = (6 + 7 + 10 + 12 + 13 + 4 + 8 + 12)/8 = 72/8 = 9 है।
चरण 2: प्रेक्षणों के माध्य x̅ से क्रमशः विचलन xᵢ-x̅
अर्थात् 6 – 9, 7 – 9, 10 – 9, 12 – 9, 13 – 9, 4 – 9, 8 – 9, 12 – 9 हैं।
या –3, –2, 1, 3, 4, –5, –1, 3 हैं।
चरण 3: विचलनों के निरपेक्ष मान ।xᵢ-x̅।
3, 2, 1, 3, 4, 5, 1, 3 हैं।
चरण 4: माध्य के सापेक्ष माध्य विचलन निम्नलिखित हैः
माध्य विचलन x̅ = 1/8 ∑_(i=1)^8〖।xᵢ-x̅।〗
= (3 + 2 + 1 + 3 + 4 + 5 + 1 + 3)/8 = 22/8 = 2.75