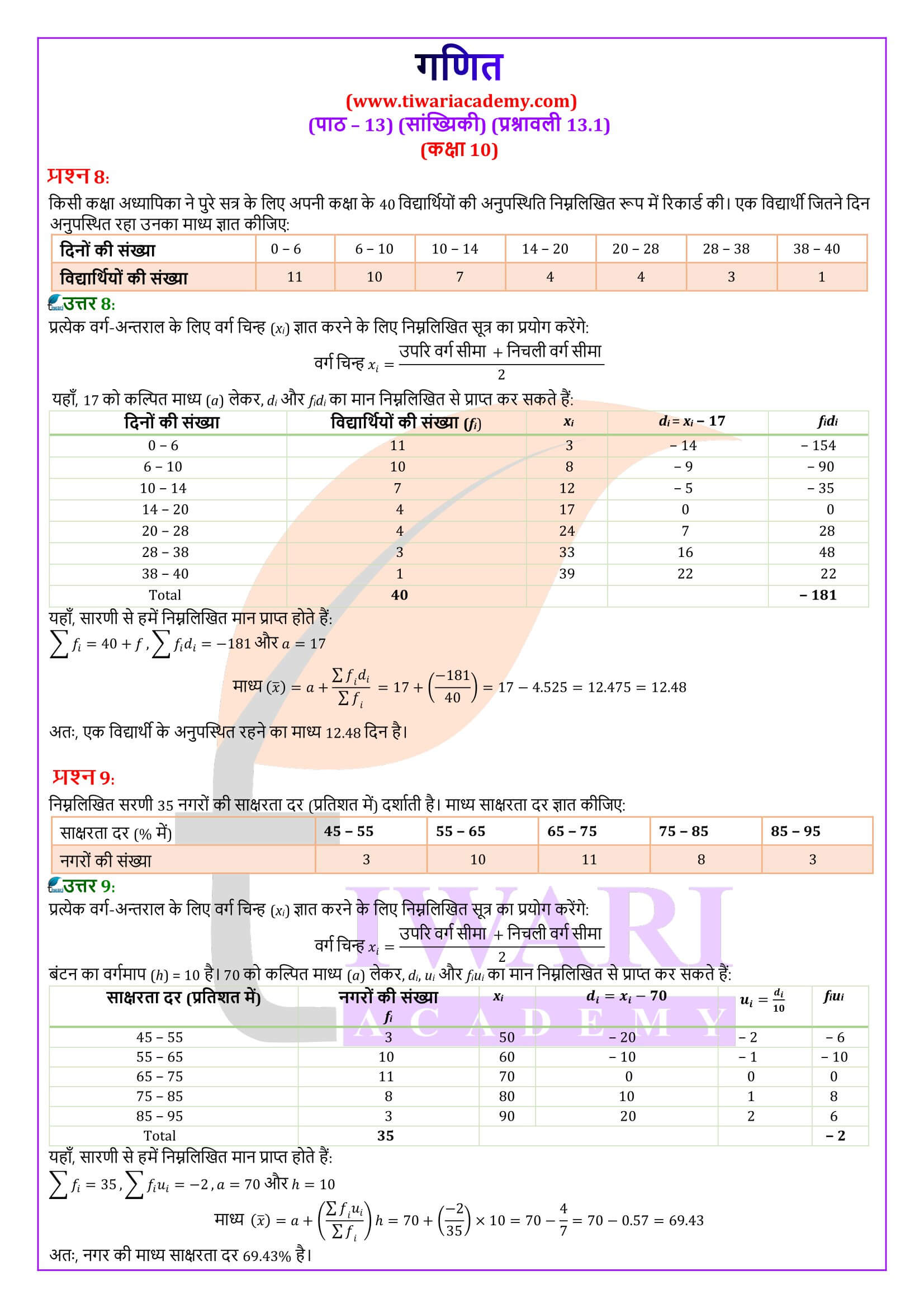
एनसीईआरटी समाधान कक्षा 10 गणित प्रश्नावली 13.1

अपरिष्कृत आँकड़ों को वर्गीकृत करने का उद्देश्य उन्हें व्यवस्थित करना है, ताकि उन्हें आसानी से आगे के सांख्यिकीय विशलेषण के योग्य बनाया जा सके। समूह या वर्ग बन जाता है।

यदि प्रेक्षणों x₁, x₂, ……….., xₙ की बारंबारताएँ क्रमशः f₁, f₂, ……….., fₙ हों, तो इसका अर्थ है कि प्रेक्षण x₁, f₁ बार आता है प्रेक्षण x₂, f₂ बार आता है, इत्यादि।
अब, सभी प्रेक्षणों के मानों का योग = f₁x₁ + f₂x₂ + ……….. + fₙxₙ है तथा प्रेक्षणों की संख्या f₁ + f₂ + ……….., + fₙ है।
अतः, इनका माध्य x निम्नलिखित द्वारा प्राप्त होगा:
x = (f₁x₁ + f₂x₂ + ……….. + fₙxₙ)/(f₁ + f₂ + ……….., + fₙ)
या माध्य x = ∑fᵢxᵢ/Σfᵢ
इसे और अधिक संक्षिप्त रूप में, x = Σfᵢxᵢ/Σfᵢ लिखते हैं, यह समझते हुए कि i का मान 1 से n तक विचरण करता है।

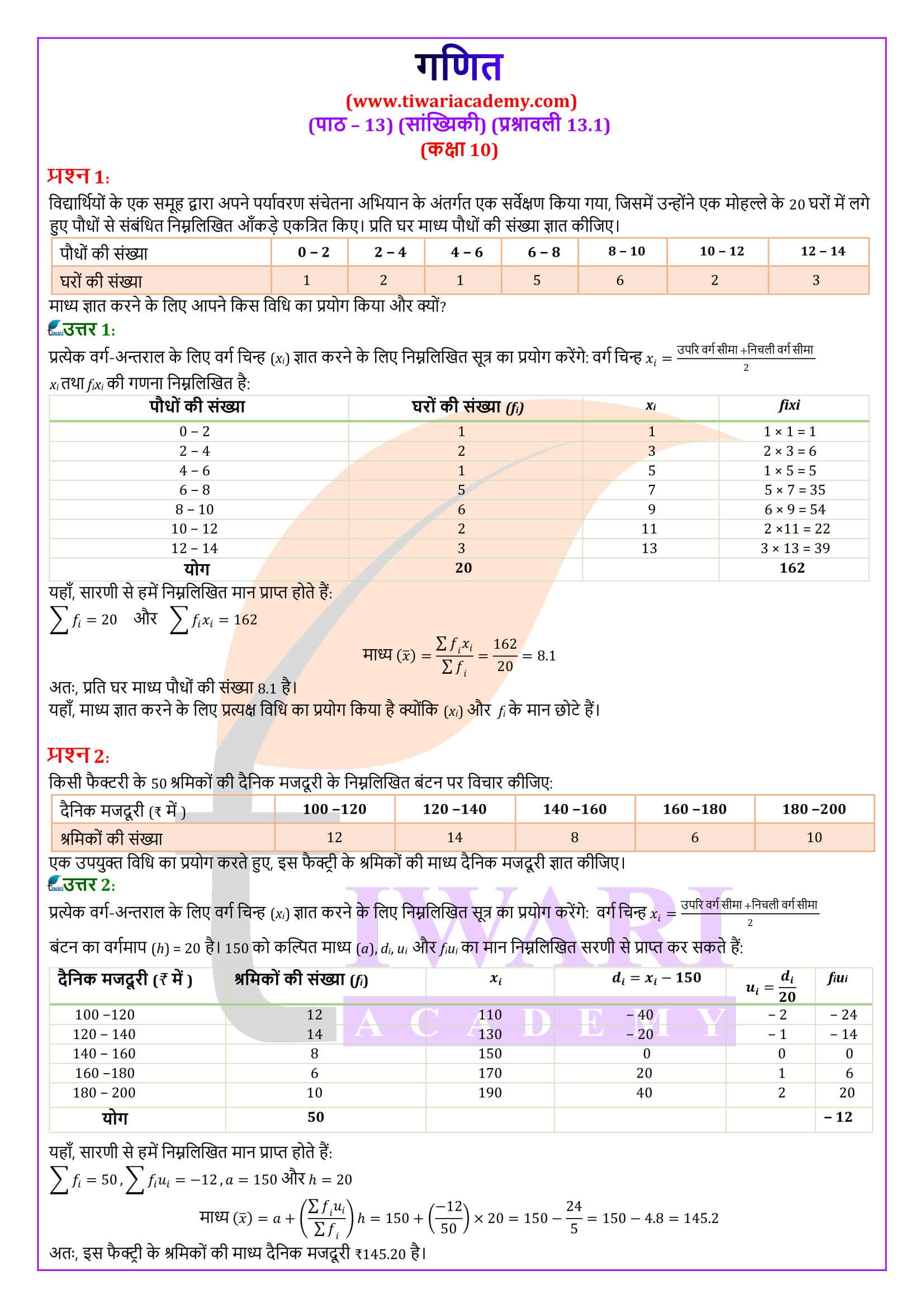
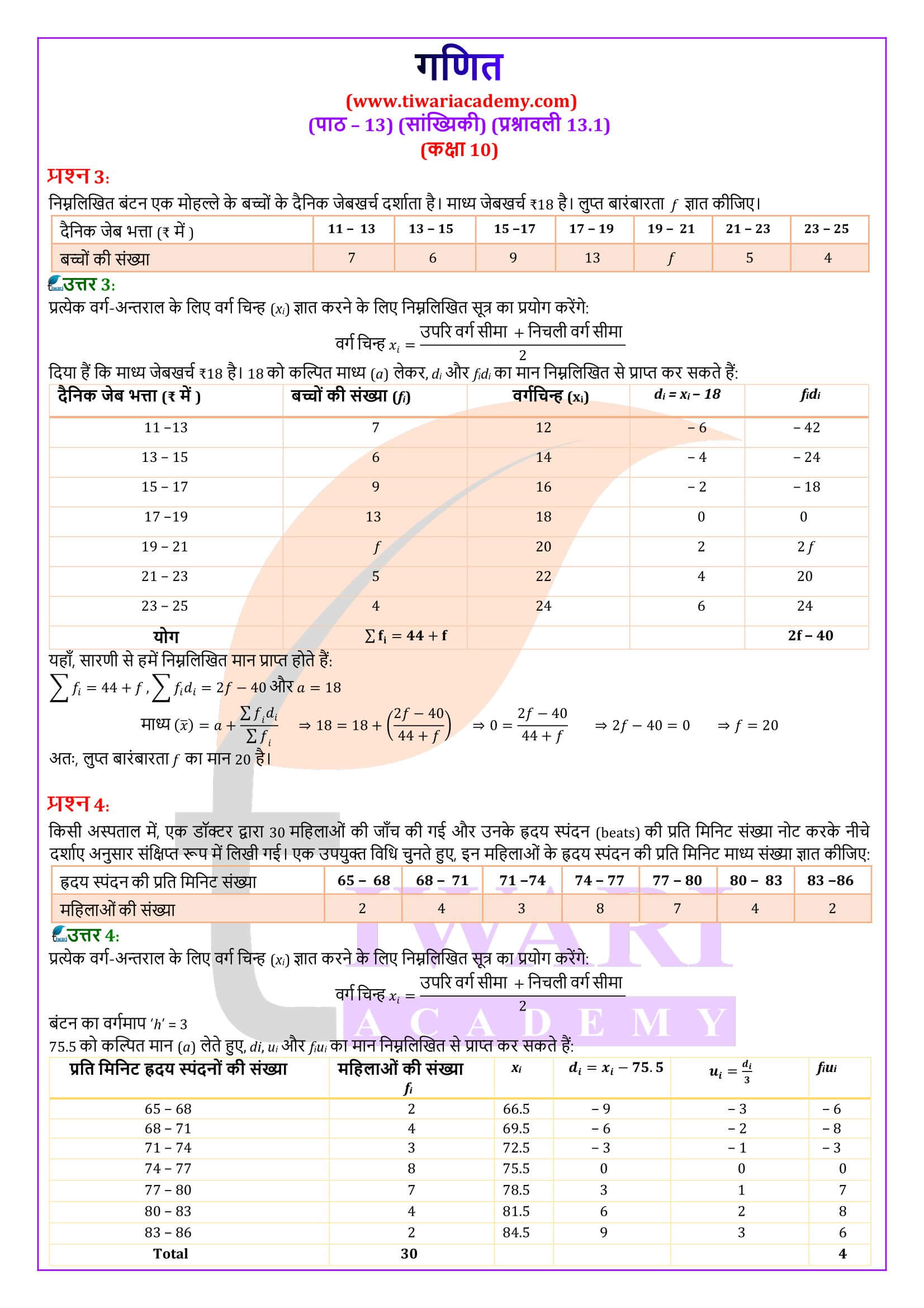
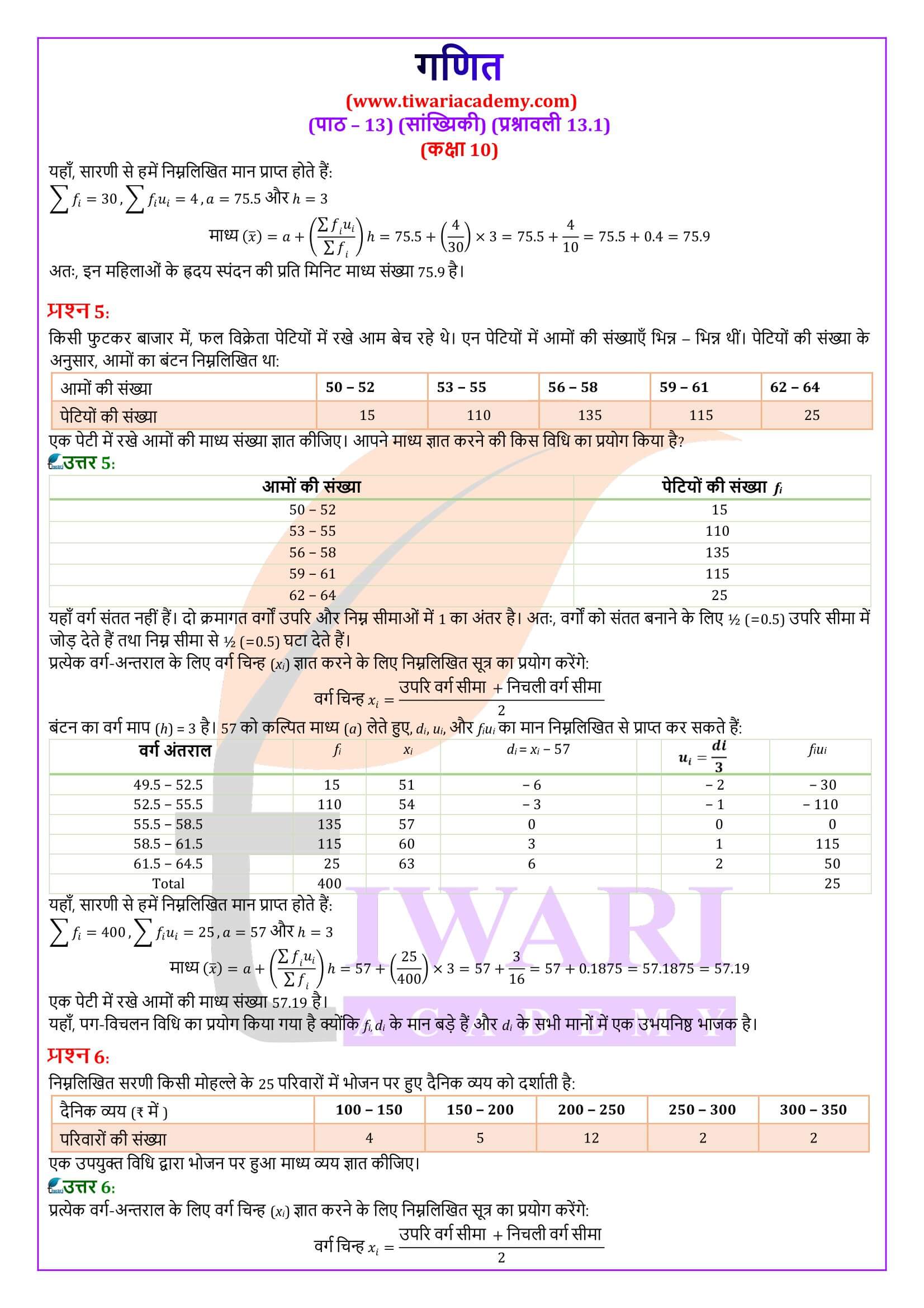
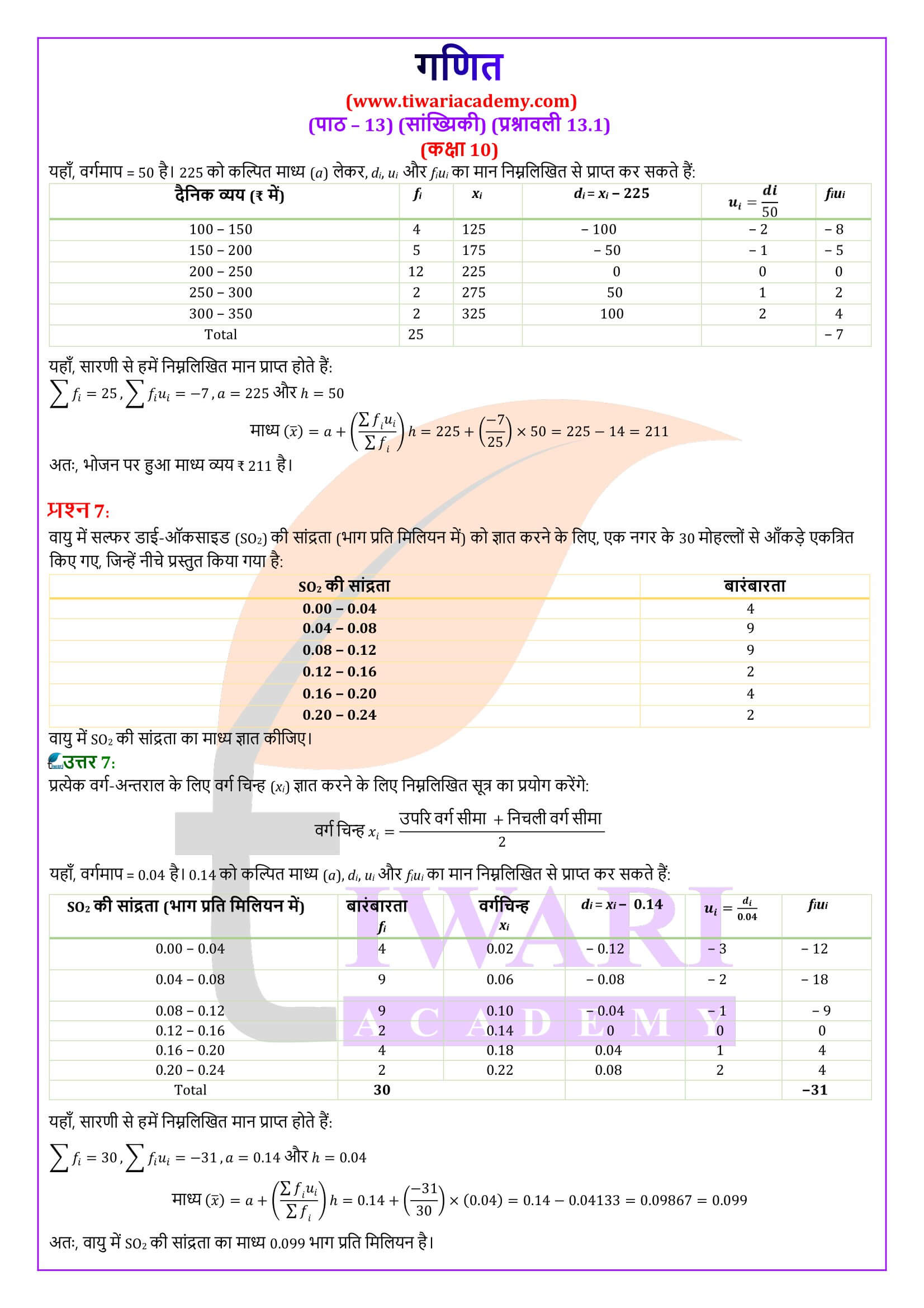
किसी स्कूल की कक्षा x के 30 विद्यार्थियों द्वारा गणित के एक पेपर में, 100 में से प्राप्त किए गए अंक, नीचे एक सारणी में दिए गए हैं। इन विद्यार्थियों द्वारा प्राप्त अंकों का माध्य ज्ञात कीजिए।
प्राप्तांक xᵢ 10 20 36 40 50 56 60 70 72 80 88 92 95
विद्यार्थियों की संख्या fᵢ 1 1 3 4 3 2 4 4 1 1 2 3 1

याद कीजिए कि माध्य ज्ञात करने के लिए, हमें प्रत्येक xᵢ से उसकी संगत बारंबारता fᵢ द्वारा गुणनफल की आवश्यकता है। अतः, इन गुणनफलों को सारणी 14-1 में दर्शाए अनुसार एक स्तंभ में रखें।
प्राप्तांक xᵢ विद्यार्थियों की संख्या fᵢ fᵢ xᵢ
10 1 10
20 1 20
36 3 108
40 4 160
50 3 150
56 2 112
60 4 240
70 4 280
72 1 72
80 1 80
88 2 176
92 3 276
95 1 95
योग Σ fᵢ = 30 Σ fᵢ xᵢ = 1779
अब, माध्य x = Σ fᵢxᵢ / Σ fᵢ
= 1779/30
= 59.3
अतः, प्राप्त किया गया माध्य अंक 59.3 है।